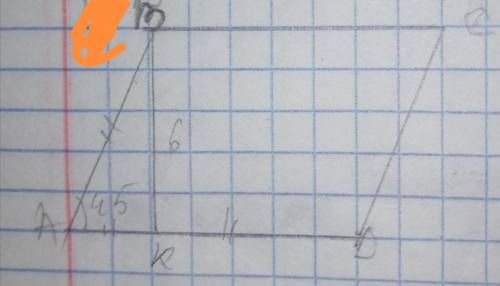
Дано авсд параллелограмм угол ВАК=45 вк =6 найти площадь авсд

Для решения этой задачи нам понадобятся знания о площади параллелограмма и тригонометрии.

1. Площадь параллелограмма можно найти, умножив длину одной из сторон на высоту, опущенную на эту сторону.

2. Для нахождения высоты параллелограмма, мы можем использовать теорему синусов в треугольнике ВАК, где угол VAB равен 90 градусов.

Давайте решим эту задачу по шагам:

Шаг 1: Найдем высоту параллелограмма
- В треугольнике ВАК известны угол ВАК (45 градусов) и длина стороны ВК (6).
- Для нахождения высоты, нам понадобится знать длину стороны ВА.
- Так как параллелограммы имеют противоположные стороны равными и параллельными, то длина стороны ВА будет равна длине стороны ВК.
- Итак, длина стороны ВА = 6.

Шаг 2: Найдем высоту треугольника ВАК
- Используем теорему синусов: синус угла (45 градусов) равен отношению противолежащей стороны (высоты) к гипотенузе (ВК).
- Подставляем известные значения и находим высоту: синус(45 градусов) = высота / 6.
- Высота = 6 * синус(45 градусов).

Шаг 3: Найдем площадь параллелограмма
- Площадь равна произведению длины стороны ВА на высоту.
- Подставляем известные значения: площадь = 6 * 6 * синус(45 градусов).

Шаг 4: Найдем численное значение площади
- Для этого нам потребуется знать значение синуса 45 градусов.
- Синус(45 градусов) равен 0.707.
- Теперь мы можем найти численное значение площади: площадь = 6 * 6 * 0.707.

Шаг 5: Найдем окончательный ответ
- Выполняем вычисления: площадь = 36 * 0.707.
- Площадь примерно равна 25.51 (округляем до двух десятичных знаков)

Итак, площадь параллелограмма АВСД примерно равна 25.51.