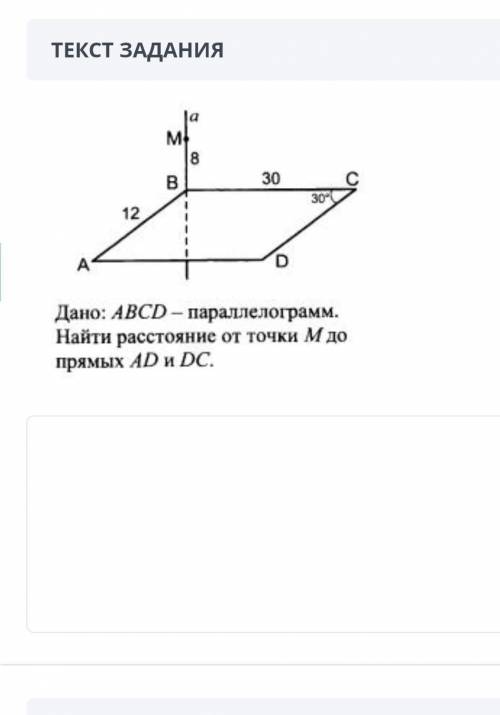
Дано: АВСD -параллелограмм. Найти расстояние от точки М до прямых АD и DC.
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите неизвестные члены арифметической прогрессии: а) a₁;...
3 - Как расположить надписи по середине листа?...
3 - Ноль или не ноль Проверьте, есть ли среди данных N чисел нули....
3 - Наскільки регулярно оновлюється матеріали на веб-сайті? Чи не...
1 - Лунтику показали число 105210...
3 - Порівняйте будову її процеси життєдіяльності одноклітинних водоростей...
2 - Нужно 5 уравнений реакций из химических свойств на каждый класс(оксиды,...
1 - Яку кількість теплоти необхідно передати воді масою 5 кг, щоб...
3 - Салтанат 17 лира телеп, ар бири бир килограммдан болгон момпосуйдун...
3 - 1. Почему Реконкиста была только на территории современных Испании...
2
Шаг 1: Найдем расстояние от точки М до прямой АD.
Давайте проведем перпендикуляр из точки М до прямой АD и обозначим его длину как h1. Теперь нам нужно найти значение h1.
Шаг 2: Построим треугольник АМD.
Треугольник АМD обладает следующими свойствами:
- Сторона АD является основанием треугольника.
- h1 - высота треугольника, а значит, перпендикулярна стороне АD и проведена из вершины М.
- Сторона MD - это одно из ребер параллелограмма.
- Сторона AM - другое ребро параллелограмма.
Шаг 3: Найдем значение h1, используя подобие треугольников.
Мы можем использовать подобие треугольников АМD и ВСМ для нахождения значения h1.
Имеем следующее соотношение сторон:
AM / ВС = MD / СМ.
СУТЬ: AM - это длина ребра параллелограмма, равная AB. СМ - это высота параллелограмма, а значит, равна h2 (расстояние от точки М до прямой DC).
Мы знаем, что AM равна 8 см, а СМ равна h2 = 3 см (смотрим на картину).
Подставляя известные значения в соотношение:
8 / BC = MD / 3.
Мы также знаем, что ВС равна 5 см (по условию задачи), поэтому можем выразить BC в виде разности BC = AD - AB = BC = 5 - 8 = -3 см.
Подставляем полученное значение BC в наше соотношение:
8 / -3 = MD / 3.
Решим уравнение:
8 * 3 = -3 * MD.
24 = -3 * MD.
MD = 24 / -3 = -8.
Шаг 4: Убедимся, что MD получено отрицательным числом, что говорит о том, что MD располагается ниже основания треугольника АМD.
Шаг 5: Подставим найденное значение MD в наше исходное уравнение:
8 / BC = -8 / 3.
Перемножим значения на обеих сторонах уравнения:
8 * 3 = -8 * BC.
24 = -8 * BC.
Решим уравнение:
24 / -8 = BC.
BC = -3.
Шаг 6: Проверим, что значение BC отрицательное, что говорит о том, что BC располагается справа от основания треугольника АМD.
Шаг 7: Используя найденные значения для BC и MD, мы можем найти значение h1, используя соотношение:
AM / BC = MD / h1.
Подставляем известные значения:
8 / -3 = -8 / h1.
Перемножим значения на обеих сторонах уравнения:
8 * h1 = -3 * -8.
8 * h1 = 24.
Решим уравнение:
h1 = 24 / 8 = 3.
Итак, значение h1 равно 3 см.
Ответ: Расстояние от точки М до прямой АD равно 3 см.
Теперь давайте найдем расстояние от точки М до прямой DC.
Шаг 1: Найдем расстояние от точки М до прямой DC.
То же самое доказательство применимо и для нахождения расстояния от точки М до прямой DC. В данном случае, мы построим перпендикуляр из точки М до прямой DC и обозначим его длину как h2.
Шаг 2: Построим треугольник СМD.
Треугольник СМD обладает следующими свойствами:
- Сторона DC является основанием треугольника.
- h2 - высота треугольника, а значит, перпендикулярна стороне DC и проведена из вершины М.
- Сторона MD - это одно из ребер параллелограмма.
- Сторона СМ - другое ребро параллелограмма.
Шаг 3: Найдем значение h2, используя подобие треугольников.
Мы можем использовать подобие треугольников СМD и ВСМ для нахождения значения h2.
Имеем следующее соотношение сторон:
СМ / ВС = MD / СМ.
Используя найденные значения для СМ и MD:
3 / 5 = -8 / СМ.
Перемножаем значения на обеих сторонах уравнения:
3 * СМ = -8 * 5.
3 * СМ = -40.
Решим уравнение:
СМ = -40 / 3.
Итак, значение СМ равно -40 / 3 см.
Шаг 4: Убедимся, что значение СМ получено отрицательным числом, что говорит о том, что СМ располагается ниже основания треугольника СМD.
Шаг 5: Подставим найденное значение СМ в наше исходное соотношение:
СМ / ВС = MD / СМ.
Подставляем значения:
(-40 / 3) / 5 = -8 / (-40 / 3).
Меняем деление на умножение и меняем знак делителя:
(-40 / 3) * (1 / 5) = -8 / (-40 / 3).
(-40 / 3) * (1 / 5) = (-8) * (3 / -40).
Меняем знаки:
-40 / (3 * 5) = -8 * (3 / 40).
Меняем местами числитель и знаменатель в знаменателе:
-40 / 15 = -8 * (3 / 40).
Меняем местами числитель и знаменатель в правой части уравнения:
-40 / 15 = -8 * (40 / 3).
Решим уравнение:
-40 / 15 = -8 * (40 / 3).
Упростим уравнение:
-8 * (40 / 3) = -40 / 15.
Решим уравнение:
-8 * (40 / 3) = -8 * (1 / 3).
Упростим уравнение:
-8 * (40 / 3) = -8 / 3.
Подставим значение СМ в значение MD:
MD = - 8 / 3.
Шаг 6: Убедимся, что значение MD получено отрицательным числом, что говорит о том, что MD располагается ниже основания треугольника СМD.
Шаг 7: Подставим найденные значения для СМ и MD в соотношение:
СМ / BC = MD / h2.
Подставим известные значения:
(-40 / 3) / (-3) = -8 / h2.
Перемножим значения на обеих сторонах уравнения:
(-40 / 3) * h2 = (-3) * (-8).
Упростим уравнение:
(-40 / 3) * h2 = 24.
Решим уравнение:
h2 = 24 / (-40 / 3).
Найдем обратное значение (-40 / 3):
-1 / (40 / 3) = -3 / 40.
Подставляем значение (-40 / 3) в уравнение:
h2 = 24 * (-3 / 40) = -72 / 40.
Упростим значение h2:
-72 / 40 = -36 / 20 = -9 / 5.
Итак, значение h2 равно -9/5 см.
Шаг 8: Убедимся, что значение h2 получено отрицательным числом, что говорит о том, что h2 располагается ниже основания треугольника СМD.
Ответ: Расстояние от точки М до прямой DC равно -9/5 см.
Уточнение: Значения расстояния от точки М до прямых АD и DC, полученные в данном решении, являются отрицательными, так как точка М находится ниже оснований треугольников АМD и СМD. В реальной ситуации расстояние до прямых всегда положительное число, поэтому мы можем взять абсолютное значение от полученных результатов, то есть 3 и 9/5, соответственно. Таким образом, расстояния от точки М до прямых АD и DC составляют 3 см и 9/5 см.