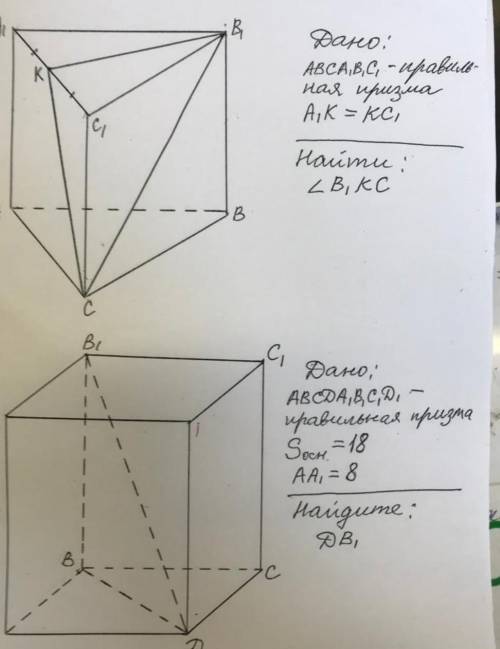
Дано АВСА1В1С1- правильная призма А1К=КС1 найти:/_В1 КС

Правильная призма АВСА1В1С1 представляет собой трехгранный многогранник, у которого вершины А, В и С соединены ребрами с вершинами А1, В1 и С1 соответственно. Также известно, что сторона призмы А1К равна стороне КС1.

Для нахождения искомого угла \(\angle В1КС\) нужно использовать свойство параллельных перпендикуляров: если две прямые AB и CD параллельны, а PQ — перпендикуляр к ним обеим, то угол между PQ и любой из прямых AB или CD будет равен углу между PQ и другой прямой.

Исходя из этой информации, можно сделать следующие выводы:
1. Стороны А1В1 и СК1 являются параллельными и равными.
2. Стороны АВ и КС являются параллельными и равными.

Таким образом, треугольники А1В1К и В1КС равные. Из этого следует, что их углы между сторонами КА1 и КS также равны.

Обозначим угол \(\angle В1КС\) как \(\alpha\).

Имеем:
\(\angle В1КС = \alpha\)
\(\angle А1В1К = \angle БАВ1\) (углы треугольников равны)
\(\angle БАВ1 = \angle САС1\) (углы равны, так как стороны равные)
\(\angle САС1 = \angle КСА1\) (углы равны, так как стороны равные)
Таким образом, угол \(\angle В1КС\) равен углу \(\angle КСА1\), который обозначен как \(\alpha\).

Ответ: угол \(\angle В1КС\) равен углу \(\angle КСА1\), который обозначается как \(\alpha\).