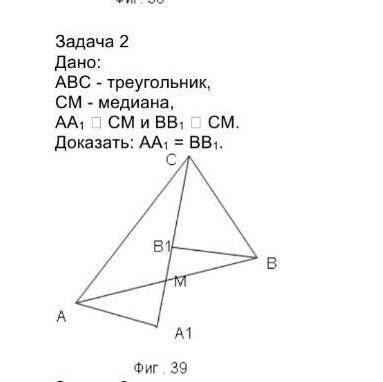
Дано:
АВС - треугольник,
СМ- медиана,
АА1 СМ и BB1 СМ.
Дакозать: АА1=ВВ1​

Для доказательства равенства AA1=BB1, воспользуемся свойством медианы, которое заключается в том, что медиана делит сторону треугольника пополам и создает два равных отрезка.

Обратимся к треугольнику АВС. Поскольку СМ - медиана, она делит сторону АВ пополам и создает два равных отрезка - АМ и МВ.

Теперь рассмотрим треугольник АА1СМ. По условию, АА1 - отрезок, который пересекает медиану СМ. Поскольку медиана СМ делит сторону АВ пополам, то она также делит сторону АА1 пополам. Таким образом, получаем, что АМ=МА1.

Аналогичное рассуждение можно провести для треугольника ВВ1СМ и доказать, что МВ=МB1.

Таким образом, мы получили, что АМ=МА1 и МВ=МB1, что означает, что отрезки АА1 и ВВ1 равны между собой.

Итак, мы доказали, что АА1=ВВ1.