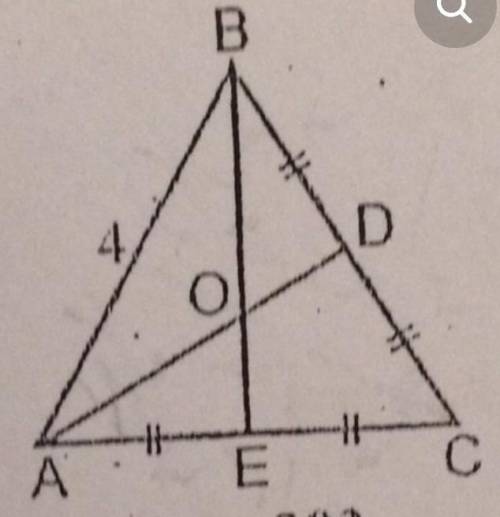
Дано АВС РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК И ЧТО НА ФОТО НАЙТИ АО,ОЕ

ОБЬЯСНИТЕ КАЖДЫЙ ШАГ В РЕШЕНИИ

Хорошо, давайте рассмотрим этот вопрос.

На данном фото изображен равносторонний треугольник АВС. Равносторонний треугольник имеет все стороны одинаковой длины и все углы равны 60 градусов.

Для того чтобы найти АО и ОЕ, нам необходимо провести определенные линии и использовать свойства равносторонних треугольников. Давайте приступим к решению:

Шаг 1: Проведем высоту треугольника. Высота треугольника - это линия, опущенная из одного из вершин на противоположную сторону и перпендикулярная этой стороне. Обозначим точку пересечения высоты треугольника и противоположной стороны как точку О.

Шаг 2: Поскольку треугольник АВС является равносторонним, все его высоты также делят его на два равных треугольника. Это означает, что длина отрезка АО равна длине отрезка ОС.

Шаг 3: Также, поскольку треугольник АВС равносторонний, все его углы равны 60 градусов. Следовательно, угол АОС также равен 60 градусов.

Шаг 4: Далее нам необходимо найти длину отрезка ОЕ. Поскольку треугольник АОЕ также является равносторонним (основанием является отрезок ОА), его углы также равны 60 градусов.

Шаг 5: Так как угол ОАЕ равен 60 градусам, то угол ОЕА тоже равен 60 градусам, так как треугольник АОЕ равносторонний. Это означает, что треугольник АОЕ является равнобедренным, и ОЕ равно ОА, а значит равно длине отрезка АО.

Таким образом, мы находимся в ситуации, когда отрезок ОА равен отрезку ОС и отрезок ОЕ также равен отрезку ОА.

Для проверки можно взять линейку и измерить длину отрезков АО и ОЕ, чтобы убедиться, что они равны.

Надеюсь, это решение понятно для вас, и вы смогли разобраться в данной геометрической задаче. Если у вас возникнут дополнительные вопросы, пожалуйста, не стесняйтесь задавать их.