Дано: АС || ВD, АВ = АС,
Угол АСВ = 25°.
Найти: угол DBE
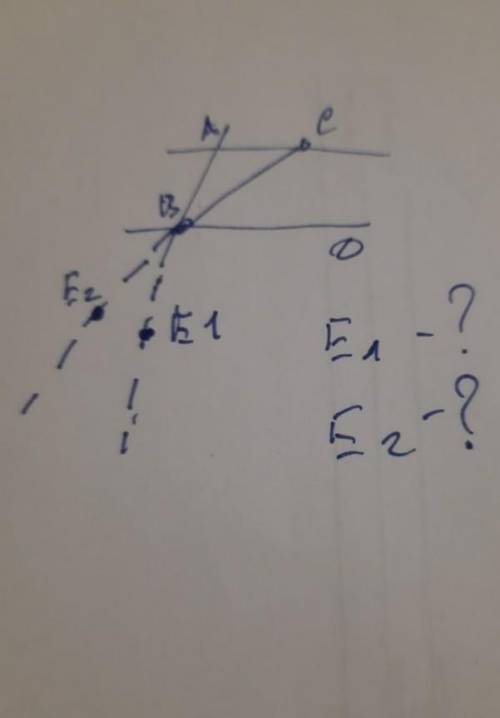
Другие вопросы по теме Геометрия
Популярные вопросы
- Составить сложный план сочинения «Настоящий добрый человек»...
2 - Как люди использовали Микролиты?...
1 - решите ребусы , кто ответит ради забаню, и по друзей забанить)...
2 - Put the verbs in brackets in the correct future tense. Justify...
1 - Пропусков в тексте. ПОБЕГПобег, состоящий из стебля, листьев...
2 - Репродукция Бродского Летний сад осенью - 5 страдательных причастий,...
3 - МӘТІНМЕН ЖҰМЫС АЙТЫЛЫМ1-тапсырма. мәтін бойынша сұрақтарға...
3 - Побудуйте графік функції y=|x|x⁴...
3 - у трикутник ABC вписано коло яке дотикається до сторін AB AC...
3 - Перепишите текст, раскрывая скобки, вставляя, где это необходимо,...
2
Исходя из условия задачи, дано, что линии АС и ВD параллельны, обозначим это как АС || ВD. Также указано, что отрезок АВ равен отрезку АС, т.е. АВ = АС. Нам нужно найти угол DBE.
1. Вспомним свойство параллельных линий: когда прямые AB и CD параллельны, а поперечная BD пересекает их, то сумма углов ABC и BCD равна 180 градусов (т.е. углы ABC и BCD являются смежными углами и их сумма равна 180°).
2. Обратимся к треугольнику АСВ. Угол В равен 25° (по условию), а угол ВСА равен 180° - 25° = 155° (т.к. у треугольника сумма всех углов равна 180°).
3. Так как линия АС параллельна линии ВD, то угол DBE и угол ВСА являются смежными углами. Значит, угол DBE = угол ВСА = 155°.
Ответ: угол DBE равен 155°.