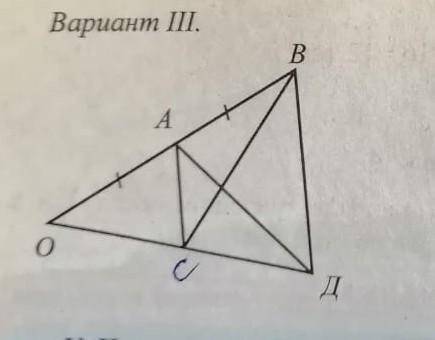
Дано: ao=ab
ac||bd
Доказать: Sobc=Soad​

Для начала, давайте разберемся с данными. У нас есть следующая информация:

1. ao=ab - это означает, что отрезок ao имеет такую же длину, как и отрезок ab.

2. ac||bd - это означает, что отрезки ac и bd параллельны друг другу.

Теперь наша задача заключается в том, чтобы доказать, что угол Sobc равен углу Soad.

Для начала, давайте посмотрим на треугольник Sobc. Из данных мы знаем, что ac||bd, поэтому мы можем использовать свойство параллельных прямых, которое гласит, что если две параллельные прямые пересекаются другими прямыми, то у соответствующих углов между этими прямыми равны.

Исходя из этого свойства, угол Sobc равен углу aoac (обозначим его как угол A). Обратите внимание, что угол A и угол Soad являются вертикальными углами, а значит они равны между собой. Поэтому, мы можем сказать, что угол Sobc равен углу Soad (Sobc = Soad).

Таким образом, мы доказали, что угол Sobc равен углу Soad с использованием свойства параллельных прямых и вертикальных углов.

Доказательство:

1. ao=ab (дано)
2. ac||bd (дано)
3. Sobc = aoac (свойство параллельных прямых)
4. Угол A и угол Soad являются вертикальными углами (вертикальные углы равны)
5. Sobc = Soad (4, 3)

Таким образом, мы доказали, что угол Sobc равен углу Soad.