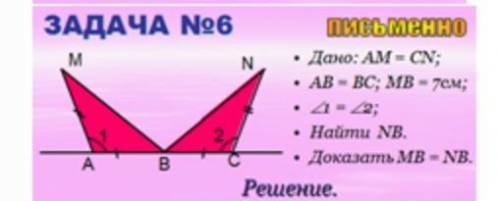
Дано AM = CN;
AB = BC; MB = 7см;
<1 = <2
Найдите NB
Доказать MB = NB
не письмо
​

Для решения данной задачи, начнем с построения вспомогательной фигуры для наглядности.

1. Возьмем точку D на прямой AM так, чтобы AD = AB (так как AB = BC).
2. Проведем прямую DN параллельную прямой BC, соединяющую точки D и N.
3. Проведем прямую CM. Так как AM = CN, то эта прямая будет перпендикулярна прямой DN.

Теперь, посмотрим на получившуюся фигуру:

A____________________C
/| |\
/ | | \
/ | ΔADM | \
/___|_________D_________|___\
B M N

Из построения, мы можем заметить следующее:
1. ΔADM и ΔCND - равнобедренные треугольники, так как AM = CN и AD = AB. Также, у них равны основания MD = CD.
2. Прямые DM и CN являются высотами, опущенными на основания треугольников ΔADM и ΔCND соответственно.

Теперь, рассмотрим следующие равенства углов:

1. Угол 1 = угол 2 (данное условие).
2. Угол 3 = 90° (так как прямая CN перпендикулярна прямой DN).
3. Угол 4 = угол 5 (так как углы при основаниях равнобедренного треугольника ΔADM равны).

Рассмотрим теперь треугольник ΔDNC. У нас есть следующие равенства углов:

1. Угол 2 = 180° - угол 5 - угол 3 (сумма углов треугольника равна 180°).
2. Угол 3 = 90°.
3. Угол 2 = 180° - угол 5 - 90°.
4. Угол 2 = 90° - угол 5.

Таким образом, мы получили, что угол 2 равен 90° - угол 5.

Из угловой теоремы, мы знаем, что сумма углов в треугольнике равна 180°. Значит, угол 2 + угол 1 + угол 4 = 180°.
Подставим в это равенство выражение, которое мы получили для угла 2.

90° - угол 5 + угол 1 + угол 4 = 180°.

Теперь, заметим что угол 1 = угол 2 (данное условие).

90° - угол 5 + угол 2 + угол 4 = 180°.

90° + угол 2 - угол 5 + угол 4 = 180°.

Угол 2 + угол 4 = угол 5 + 90°.

Теперь, заметим что угол 4 = угол 5 (из равнобедренности ΔADM).

Угол 2 + угол 4 = угол 5 + 90°.

Угол 2 = 90°.

Таким образом, мы доказали, что угол 2 равен 90°.

Теперь, посмотрим на треугольник ΔMNB. У нас есть следующие равенства углов:

1. Угол 1 = угол 2 (доказано выше).
2. Угол 6 = 90° (так как прямая NB перпендикулярна прямой DN).
3. Угол 2 = 90° (доказано выше).

Из этих равенств, мы получаем, что угол 1 = угол 6 = 90°.

Таким образом, треугольник ΔMNB является прямоугольным треугольником со стороной MB равной стороне NB.

Итак, мы доказали, что MB = NB.