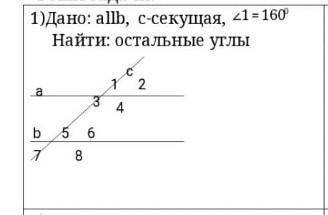
Дано: аllb, с-секущая, угол 1 = 160°
Найти: остальные углы
Другие вопросы по теме Геометрия
Популярные вопросы
- Предложение о котором можно сказать верно оно или нет...
3 - Напишите сочинение на тему степа дрова колет. заранее 20...
3 - Текст о весне (3 4 предложения ) с предлогами о и об...
1 - Решите уравнение: 1,8*(-4)-у=2,8 решите...
2 - Как относились разведчики и капитан енакиев о ване...
2 - Найдите графическим решение системы : {3у=-2х,{2х+у=-4. решите...
2 - Почему у разных видов рыб срок вынашивания икринки разный?...
1 - Дайте определение словосочетанию и расскажите о строении словосочетании....
3 - Решить собака погналась за кроликом находящимся от нее в 150...
2 - Сумма числителя и знаменателя равна 4140. после сокращения получилась...
3
Первое, что нам следует сделать, это найти угол 2, который является смежным с углом 1, так как они оба образованы секущей allb.
Смежные углы - это углы, которые имеют общую сторону и одну общую вершину. В нашем случае, уголы 1 и 2 имеют общую сторону ab и общую вершину b. Таким образом, угол 2 равен 160°.
Теперь мы можем использовать свойство секущей, которое гласит, что сумма углов, лежащих внутри фигуры, образованной секущей, равна 180°.
У нас есть угол 2, который равен 160°, и мы хотим найти остальные углы, которые обозначены как углы 3, 4 и 5.
Сумма углов 2, 3, 4 и 5 должна равняться 180°.
Таким образом, мы можем записать уравнение:
160° + угол 3 + угол 4 + угол 5 = 180°
Теперь, выразим угол 3:
угол 3 = 180° - 160° - угол 4 - угол 5
Мы можем записать угол 4 и угол 5 в виде алгебраических выражений, используя свойство соответствующих углов.
Соответствующие углы - это пары углов, расположенных на одной стороне секущей и на одной стороне пересекаемой линии. В нашем случае, угол 4 и угол 5 образуются пересекаемой линией bc и секущей allb.
Угол 4 является соответствующим углом к углу 2 и, следовательно, равен 160°.
Угол 5 также является соответствующим углом к углу 2 и, следовательно, равен 160°.
Теперь мы можем заменить значения угла 4 и угла 5 в нашем уравнении:
угол 3 = 180° - 160° - 160° - 160°
Теперь мы можем решить это уравнение:
угол 3 = -300°
Однако, углы не могут быть отрицательными, поэтому нам нужно изменить знак угла 3.
Если мы заменим угол 4 и угол 5 значениями соответственно 160°, то у нас получится:
угол 3 = 180° - 160° - 160° - 160° = 180° - 480° = -300°
Однако, углы не могут быть больше 180°, поэтому мы должны использовать другие свойства, чтобы найти правильные значения углов.
Изучим еще раз нашу схему. В секущей allb имеются две пары соответственных углов. Это углы 3 и 7, а также углы 4 и 5.
Так как углы 4 и 5 равны, это означает, что углы 3 и 7 также должны быть равными.
Таким образом, угол 3 равен углу 3 и угол 7 равен углу 3.
Если мы заменим значениями угла 3 наше уравнение:
угол 3 = 180° - 160° - угол 3 - угол 3
Мы можем объединить углы 3 слева и справа:
2 * угол 3 = 180° - 160°
2 * угол 3 = 20°
Теперь делим обе стороны на 2:
угол 3 = 10°
Таким образом, мы нашли значение угла 3, которое равно 10°.
Теперь, чтобы найти угол 4 и угол 5, мы можем использовать свойства соответствующих углов.
Угол 4 является соответствующим углом к углу 2, который равен 160°.
Угол 5 также является соответствующим углом к углу 2, который также равен 160°.
Таким образом, значения угла 4 и угла 5 равны соответственно 160° и 160°.
То есть, углы 4 и 5 равны 160°.
Итак, мы нашли остальные углы:
Угол 1 = 160°, угол 2 = 160°, угол 3 = 10°, угол 4 = 160°, угол 5 = 160°, угол 7 = 10°.