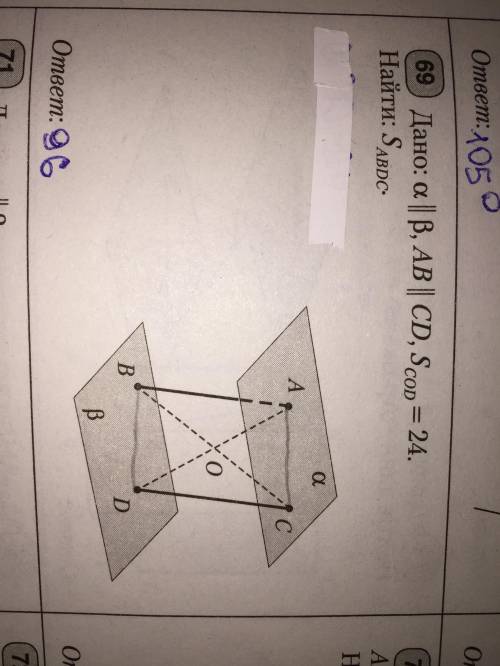
Дано:альфа параллельна бета, AB параллельна CD, Scod=24. Найти Sabc

Для решения этой задачи нам нужно использовать свойства параллельных прямых и площадей подобных треугольников.

Согласно условию задачи, альфа (α) и бета (β) параллельны, а также сторона AB параллельна стороне CD. Также нам известно, что площадь треугольника S_cod равна 24.

Для начала, обратим внимание на теорему о площадях подобных треугольников, которая утверждает, что если два треугольника подобны, то отношение площадей этих треугольников равно квадрату отношения длин соответствующих сторон.

Мы знаем, что треугольники ABC и COD подобны, так как у них все углы равны (параллельные прямые создают равные углы). Поэтому отношение их площадей равно квадрату отношения длин соответствующих сторон.

Таким образом, мы можем записать следующее соотношение:
S_abc / S_cod = (AC / CO)^2

Теперь давайте проведем линии AD и BC, обозначим точку их пересечения как E. Заметим, что треугольник ADE подобен треугольнику CBE, так как у них все углы равны, а стороны AD и CB параллельны.

Обозначим длину AD как x и длину CB как y.

Теперь у нас есть следующее соотношение:
S_abc / S_cod = (AC / CO)^2 = (AE / CO)^2

Нам нужно найти площадь треугольника ABC (S_abc).

Мы можем использовать понятие пропорций для нахождения S_abc.

Заметим, что треугольники ADE и ABC также подобны, потому что у них все углы равны, а стороны AD и AB параллельны.
Таким образом, мы можем записать следующее соотношение:
S_abc / S_ade = (AB / AD)^2

Также мы знаем, что площадь треугольника ADE равна половине площади треугольника COD, то есть S_ade = S_cod / 2.

Подставляя это соотношение в предыдущую формулу, получаем:
S_abc / (S_cod / 2) = (AB / AD)^2

Теперь мы можем заметить, что AB / AD = AE / CO, так как треугольники ADE и ABC подобны и соответствующие стороны пропорциональны.

Итак, мы получаем следующее соотношение:
S_abc / (S_cod / 2) = (AE / CO)^2

Мы знаем, что S_cod = 24, поэтому можем продолжить вычисления:
S_abc / (24 / 2) = (AE / CO)^2
S_abc / 12 = (AE / CO)^2

Теперь мы должны найти отношение AE / CO.

Обратим внимание на треугольники AEB и COB. Они также подобны, так как у них все углы равны, а стороны AB и BC параллельны.

Мы можем использовать отношение сторон AE / CO равное AB / BC.

Таким образом, поскольку AB = 3 и BC = 6, получаем:
AE / CO = 3 / 6 = 1 / 2

Подставляя это значение в предыдущую формулу, получаем:
S_abc / 12 = (1 / 2)^2
S_abc / 12 = 1 / 4

Чтобы найти S_abc, умножим обе части уравнения на 12:
S_abc = 12 * (1 / 4) = 12 / 4 = 3

Таким образом, ответ: S_abc = 3.