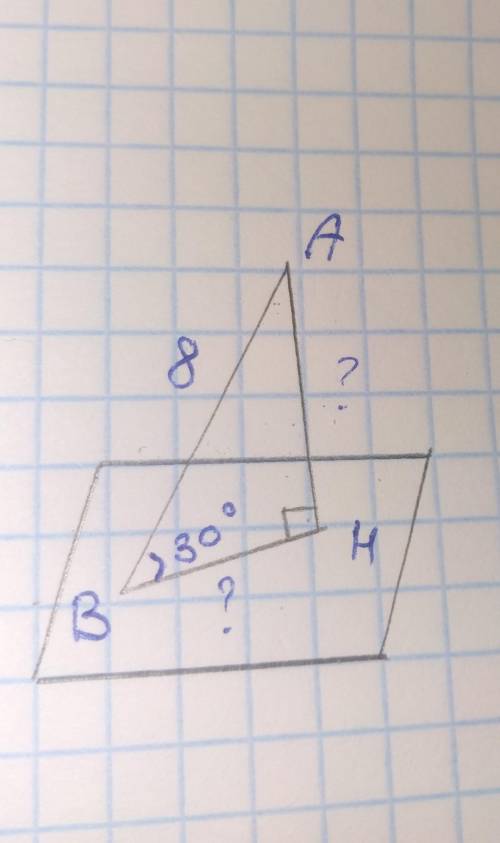
дано: AH перпен. (a)
AB -наклонная
найти: AH и BH​

Для решения этой задачи, нам понадобится использовать основные свойства перпендикуляров и треугольника.

По условию, имеем прямую AH, которая является перпендикуляром к отрезку AB. То есть, угол между AH и AB равен 90 градусов.

Для начала, обозначим точку пересечения прямых AH и AB как точку D.

Также, обозначим отрезок BD как x.

Теперь мы можем составить уравнение треугольника ABD для нахождения отрезков AH и BH.

В этом треугольнике у нас есть следующие известные данные:
- AB - наклонная сторона треугольника
- AD и BD - катеты треугольника

Применим теорему Пифагора для треугольника ABD:

AB^2 = AD^2 + BD^2

AB^2 = x^2 + AH^2

Теперь, мы имеем еще одно соотношение, которое у нас есть - AH является перпендикуляром к AB. Это означает, что угол BAD также является прямым углом.

Таким образом, треугольник ABD является прямоугольным треугольником. Мы можем использовать тригонометрическую функцию тангенса для нахождения отношения между сторонами.

tg(BAD) = AD/BD

Используя обозначение x для BD, мы можем записать это уравнение:

tg(90 градусов) = AD/x

tg(90 градусов) = AH/AB

Так как тангенс 90 градусов равен бесконечности, получаем:

бесконечность = AH/AB

Это означает, что отношение между AH и AB является неопределенным, а значит AH может быть любым значением, при условии, что AB не равно нулю.

Таким образом, мы не можем однозначно определить значения AH и BH по данным условиям задачи. AH может принимать любое значение, а BH будет зависеть от выбранного значения AH.