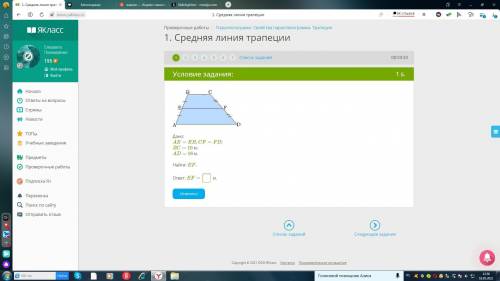
Дано:
AE=EB, CF=FD;
BC= 10 м;
AD= 16 м.

Найти: EF.

Чтобы найти значение EF, нам необходимо использовать информацию, которая дана на диаграмме и знания о свойствах треугольников.

Из условия задачи, мы знаем, что AE = EB и CF = FD. Это означает, что треугольник ABC является равнобедренным, и треугольник ADF тоже является равнобедренным.

Также, у нас есть измеренные стороны BC = 10 м и AD = 16 м. Давайте воспользуемся этой информацией.

Мы можем разделить сторону BC пополам, получив отрезок BE. Теперь у нас есть два равных отрезка: AE и EB.

Поскольку AB и AC это боковые стороны равнобедренного треугольника ABC, мы можем сделать вывод, что углы BAC и ABC должны быть равными. Также, по свойству равнобедренного треугольника, высота, опущенная из вершины A, будет являться медианой и медианой будут параллельны боковым сторонам. Поэтому AE параллельно BC и AEBC будет параллелограммом.

Расстояние между прямыми параллельными сторонами параллелограмма равно высоте параллелограмма. Из свойств медианы, мы знаем, что высота параллелограмма делит противоположную сторону на две равные части. Таким образом, AE = BC / 2 = 10 / 2 = 5 м.

Теперь мы можем использовать эти равные отрезки AE и EB для нахождения длины стороны AB. AB = AE + EB = 5 + 5 = 10 м.

Мы также знаем, что AD = 16 м. Так как треугольник ADF является равнобедренным, мы можем установить, что AF = AD = 16 м.

Итак, теперь у нас есть два равных отрезка AB = 10 м и AF = 16 м. Мы можем найти длину отрезка BF, применив теорему Пифагора к треугольнику ABF.

По теореме Пифагора, гипотенуза в квадрате равна сумме квадратов двух катетов. В нашем случае, AB это гипотенуза, AF это один катет, и BF это другой катет. Поэтому мы можем записать уравнение:

AB² = AF² + BF²

10² = 16² + BF²

100 - 256 = BF²

BF² = -156

Так как нет реального значения, которое удовлетворяет этому уравнению, у нас проблема. Мы не можем найти точное значение для BF.

Теперь давайте рассмотрим треугольник CEF. Мы знаем, что CF = FD и мы знаем, что эти отрезки равны 5 м.

Также, мы знаем, что треугольникы CEF и ABC подобны. Это означает, что соответствующие стороны этих треугольников пропорциональны.

Мы можем составить пропорцию между сторонами этих треугольников с использованием известных значений:

CE / BC = EF / AB

CE / 10 = EF / 10

CE = EF

Таким образом, EF = 5 м.

Вывод: Длина отрезка EF равна 5 м.