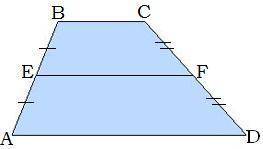
Дано:
AE=EB, CF=FD;
BC= 10 м;
AD= 14 м.
Найти: EF

ответ: EF=

Чтобы найти значение EF, давайте посмотрим на данную нам информацию.

Мы знаем, что AE=EB и CF=FD. Это означает, что отрезки AE и EB равны по длине, а также отрезки CF и FD равны по длине.

У нас также есть информация, что BC=10 м и AD=14 м.

На основе данной информации мы можем использовать теорему Пифагора для треугольников ABC и ADE.

Теорема Пифагора говорит нам, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

В треугольнике ABC, AB является гипотенузой, BC является одним катетом, поэтому мы можем записать:

AB^2 = BC^2 + AC^2

AB^2 = 10^2 + AC^2

AB^2 = 100 + AC^2

Также, в треугольнике ADE, AD является гипотенузой, AE является одним катетом, поэтому мы можем записать:

AD^2 = AE^2 + DE^2

AD^2 = AE^2 + (AC + CE)^2

AD^2 = AE^2 + AC^2 + 2(AC)(CE) + CE^2

AD^2 = AE^2 + AC^2 + 2(AC)(CE) + CE^2

AD^2 = AE^2 + AC^2 + (2AC)(CE) + CE^2

Теперь мы можем заменить AE и CE на EB и FD соответственно, потому что по условию они равны, и получим:

AD^2 = EB^2 + AC^2 + (2AC)(FD) + FD^2

14^2 = EB^2 + AC^2 + (2AC)(FD) + FD^2

196 = EB^2 + AC^2 + (2AC)(FD) + FD^2

EB^2 = 196 - AC^2 - (2AC)(FD) + FD^2

Теперь мы можем заменить EB на AE, потому что они также равны, и получим:

AE^2 = 196 - AC^2 - (2AC)(FD) + FD^2

AE^2 = 196 - AC^2 - 2ACFD + FD^2

Теперь мы можем использовать информацию, что AE=EB и CF=FD, чтобы упростить выражение:

EB^2 = 196 - AC^2 - 2ACFD + FD^2

EB^2 = 196 - AC^2 - 2AC(CF) + CF^2

EB^2 = 196 - AC^2 - 2AC^2 + CF^2

EB^2 = 196 - 3AC^2 + CF^2

EB^2 = 196 - 3(BC^2 - AC^2) + CF^2

EB^2 = 196 - 3(10^2 - AC^2) + CF^2

EB^2 = 196 - 3(100 - AC^2) + CF^2

EB^2 = 196 - 300 + 3AC^2 + CF^2

EB^2 = 196 - 300 + 3AC^2 + (BC^2 - AC^2)

EB^2 = 196 - 300 + 3AC^2 + (10^2 - AC^2)

EB^2 = 196 - 300 + 3AC^2 + 100 - AC^2

EB^2 = 96 + 2AC^2

Таким образом, мы нашли значение EB^2, и теперь можем выразить EB:

EB = √(96 + 2AC^2)

Теперь, когда мы знаем значение EB, мы можем найти значение EF, используя информацию, что EF = EB + FD:

EF = √(96 + 2AC^2) + CF

EF = √(96 + 2AC^2) + FD

EF = √(96 + 2AC^2) + FD

EF = √(96 + 2(BC^2 - AC^2)) + CF

EF = √(96 + 2(10^2 - AC^2)) + CF

EF = √(96 + 2(100 - AC^2)) + CF

EF = √(96 + 200 - 2AC^2) + CF

EF = √(296 - 2AC^2) + CF

Таким образом, ответом на вопрос является EF = √(296 - 2AC^2) + CF.

При решении мы использовали данную информацию о равенстве отрезков AE=EB и CF=FD, а также применили теорему Пифагора и свойства алгебры для выведения конечного ответа.