Дано: AD перпендикулярно AC, AC перпендикулярно AB, BD перпендикулярно CB. Докажите, что BD перпендикулярно пл(ABC).
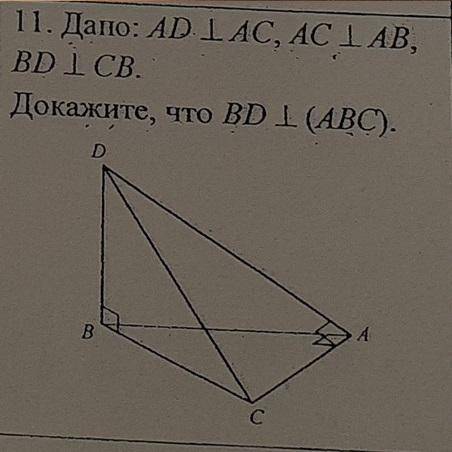
Ответы
Добрый день! Давайте разберемся с этой задачей.
У нас дано, что AD перпендикулярно AC, AC перпендикулярно AB и BD перпендикулярно CB. Нам нужно доказать, что BD перпендикулярно плоскости ABC.
Для начала, давайте вспомним основные свойства перпендикуляров. Перпендикуляр – это линия, которая образует прямой угол с другой линией или плоскостью. Прямой угол равен 90 градусам, то есть это прямая линия, которая делит угол на две равные части.
Мы видим, что AD и AC перпендикулярны между собой и также перпендикулярны к прямым линиям AB и CB с соответствующими точками пересечения D и C.
Теперь давайте предположим, что прямая BD не перпендикулярна плоскости ABC. Это означает, что линия BD и плоскость ABC пересекаются под некоторым углом, отличным от 90 градусов.
Если линия BD и плоскость ABC пересекаются, то существует хотя бы одна точка пересечения E между ними.
Теперь давайте рассмотрим треугольник BDE. У нас есть два перпендикуляра: BD и BE, так как плоскость ABC пересекает линию BD под углом отличным от 90 градусов.
Это противоречие, так как в треугольнике BDE угол между перпендикулярами BD и BE должен быть прямым углом (равным 90 градусам). Но наше предположение о том, что прямая BD не перпендикулярна плоскости ABC, привело к тому, что угол между BD и BE не равен 90 градусам.
Из этого следует, что наше предположение неверно и линия BD действительно перпендикулярна плоскости ABC.
Таким образом, мы доказали, что BD перпендикулярно плоскости ABC.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Особенности сочетания компонентов природы средней сибири и причины этих особенностей...
3 - Сколько граммов сахара и воды нужно взять, что бы приготовить 500 гр 70%го раствора...
3 - Вставить пропущенные буквы.поставь знаки препинания в конце предложений.назови...
3 - Раздели слова на слоги. поставь удорение. сова ворона мосты сом...
3 - Выложите мне самый сложный пример в мире !...
2 - Носит одуванчик..сарафанчик.подрастет, нарядится в ветерку послушное...
3 - Какие события повторяются в сказке аленький цветочек...
1 - 15 ! диагональ ac прямоугольника abcd=3 см и состовляет со стороной adугол30радусов.найти...
1 - Заранее . установите соответствие. сокр. ионное уравнение: 1.nh+(4)+oh=nh(3)стрелка...
2 - Инструкция с отрицательными ! ! 40 !...
2