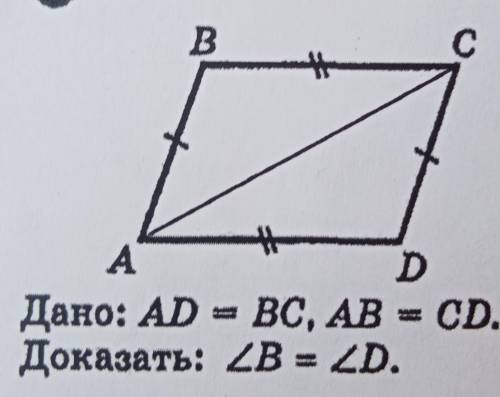
Дано: AD = BC, AB = CD. Доказать: 2B = 2D.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какую скорость приобрести ракета,движущаяся из состояния покоя с ускорением...
3 - Переведите мақсатына өзін өзі жетілдіру арқылы жетеді. өзін-өзі жетілдіру...
1 - Округлите 256.903.786 а)до десятков б)до сотен в)до тысяч заранее !...
3 - Решите : a) (21,2544: 0,9+1,02*3,2): 5,6 cтолбикам б) 4,36: (3,15+2,3)+(0,792-0,78)*350...
3 - На пару через 3 (2/3+5/6): 1/21+3,9*0,5...
3 - 1. могли бы вы описать себя в 5 словах? 2. что бы вы хотели изменить в...
3 - Кматериальной точке приложены две силы 3h и 4h под прямым углом друг другу...
3 - Найти область определения функции 1)f(x)=x/(x³+8)(x-3)² 2)f(x)=1/x-3...
2 - Какие из следующих утверждений верные: 1) для каждого натурального числа...
3 - Почему не называются класс тысяч в числе 8 617 000 324...
3
Предположим, что координаты точек А, В, С и D следующие:
A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4).
Так как AB = CD, то расстояние между точками A и B равно расстоянию между точками C и D. Для нахождения расстояния между двумя точками можно использовать формулу расстояния между двумя точками в декартовой системе координат:
AB = √((x2 - x1)^2 + (y2 - y1)^2)
CD = √((x4 - x3)^2 + (y4 - y3)^2)
Поскольку AB = CD, то мы можем записать следующее равенство:
√((x2 - x1)^2 + (y2 - y1)^2) = √((x4 - x3)^2 + (y4 - y3)^2)
Возводим обе части уравнения в квадрат, чтобы избавиться от корней:
(x2 - x1)^2 + (y2 - y1)^2 = (x4 - x3)^2 + (y4 - y3)^2
Также, по условию задачи, AD = BC. Расстояние между точками A и D можем выразить с помощью формулы:
AD = √((x4 - x1)^2 + (y4 - y1)^2)
Расстояние между точками B и C можем выразить аналогичным образом:
BC = √((x3 - x2)^2 + (y3 - y2)^2)
По условию задачи, AD = BC, поэтому:
√((x4 - x1)^2 + (y4 - y1)^2) = √((x3 - x2)^2 + (y3 - y2)^2)
Возводим обе части уравнения в квадрат:
(x4 - x1)^2 + (y4 - y1)^2 = (x3 - x2)^2 + (y3 - y2)^2
Раскрываем скобки:
x4^2 - 2x4x1 + x1^2 + y4^2 - 2y4y1 + y1^2 = x3^2 - 2x3x2 + x2^2 + y3^2 - 2y3y2 + y2^2
Дальше, поскольку AB = CD, то AB - CD = 0. Используем это равенство:
(x2 - x1)^2 + (y2 - y1)^2 - (x4 - x3)^2 - (y4 - y3)^2 = 0
Раскрыть скобки и упростить уравнение:
x2^2 - 2x2x1 + x1^2 + y2^2 - 2y2y1 + y1^2 - x4^2 + 2x4x3 - x3^2 - y4^2 + 2y4y3 - y3^2 = 0
Теперь у нас есть два уравнения:
1) x4^2 - 2x4x1 + x1^2 + y4^2 - 2y4y1 + y1^2 = x3^2 - 2x3x2 + x2^2 + y3^2 - 2y3y2 + y2^2
2) x2^2 - 2x2x1 + x1^2 + y2^2 - 2y2y1 + y1^2 - x4^2 + 2x4x3 - x3^2 - y4^2 + 2y4y3 - y3^2 = 0
Добавим обе стороны уравнения (2) к обеим сторонам уравнения (1):
2x4x3 - 2x3x2 + 2y4y3 - 2y3y2 = 0
Делим обе части уравнения на 2:
x4x3 - x3x2 + y4y3 - y3y2 = 0
Но по условию AD = BC, поэтому мы можем записать следующее равенство:
x4x3 - x3x2 + y4y3 - y3y2 = 0
Теперь мы можем выразить 2B и 2D с помощью координат.
По определению, точка B имеет координаты (x2, y2), значит 2B будет иметь координаты (2x2, 2y2).
Аналогично, точка D имеет координаты (x3, y3), поэтому 2D будет иметь координаты (2x3, 2y3).
Так как x4x3 - x3x2 + y4y3 - y3y2 = 0, то 2B = 2D, что и требовалось доказать.