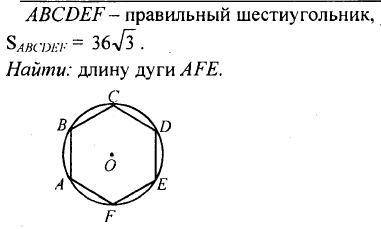
Дано: ABCDEF- правильный шестиугольник,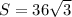
Найти: длину дуги AFE

ответ :   L = 4π√6/3  ≈  10,25 .

Пошаговое объяснение :

Нехай  АВ = а , тоді  S₆ = 6 * S ΔAOF = 6 * a² √3/4 = 36√3 ;

     a² = 2 * 36/3 = 24 ;     a² = 24 ;  a = + √24 = 2√6 ;   a = r = OA = 2√6 .

   ∪AF = ∠AOF = 60° ;   ∪AFE = ∠AOE = 2 * ∠AOF = 2 * 60° = 120° .

  Отже , градусна міра  ∪AFE = 120° , тоді  її довжина

    L = π r n/180 = π * 2√6 * 120 /180  = 4π√6/3  ≈  10,25 ;    L ≈ 10,25 .

ответ: 4π√6/3

Объяснение:

правильный шестиугольник состоит из шести правильных треугольников  со стороной,  равной радиусу описанной окружности.  площадь одного треугольника равна R²√3/4, площадь шестиугольника равна

6R²√3/4=36√3⇒R²=4*36/6=24; R=2√6, а длина окружности

l=2πR=2π*2√6=4π√6; длина дуги, подлежащая определению, составляет

2/6=1/3 от длины окружности и равна 4π√6*(1/3)=4π√6/3;