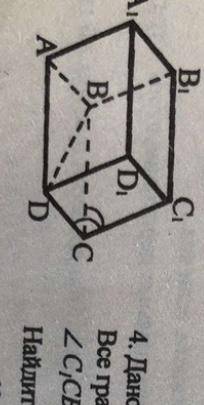
Дано: ABCDA,B,C,D, — параллелепипед, Все грани - равные ромбы.
Угол С1СВ=С1СД
Найдите угол (С1С,ВД), угол (А1С,ВД)
Другие вопросы по теме Геометрия
Популярные вопросы
- Рабочий работа по 8 часов день выполняет заданую работу за 20 дней...
2 - Написать письмо. hello, my friend! my name i am i to school. i...
2 - Решите : первое число состав 5/12 от второго, а третье число 35/72...
2 - Придумать слово из 5 букв, которое являлось бы концом одного и...
1 - Таблица по биологии 7 класс латющин 44 параграф...
2 - Назови слова с орфограммой проверяемые согласные в корне слова...
1 - Найти все значения параметра a, при которых уравнение x^10-a*|x|+a^2-a=0...
3 - 1. подготовьте аналитический письменный рассказ о матрёне тимофеевне...
1 - Какая характеристика у ильи мурамца ( багатыря)...
1 - ответьте на вопросы.в скобках есть слова.поменяйте форму слова...
3
По условию, мы знаем, что все грани параллелепипеда ABCDA,B,C,D являются равными ромбами.
1. Найдем угол (С1С,ВД):
У нас имеются две одинаковые равнобедренные трапеции: С1САВ и С1СДВ.
Так как в обоих трапециях боковые стороны равны (потому что они являются боковыми ребрами параллелепипеда), а углы описанные (угол С1СВ = угол С1СД), то и основания трапеций равны.
Зная, что все грани параллелепипеда — равные ромбы, из предыдущего утверждения следует, что СА = ВД.
Также из равнобедренности трапеции С1САВ следует, что угол (С1СА, С1ВА) равен углу (С1С, ВД), поскольку сторона ВА параллельна основанию С1СА и равна стороне С1СА.
Таким образом, угол (С1С, ВД) равен углу (С1СА, С1ВА).
2. Найдем угол (А1С, ВД):
Поскольку все грани параллелепипеда являются равными ромбами, значит сторона АВ параллельна стороне С1С, и угол (С1СА, С1ВА) равен углу (А1С, ВД).
Таким образом, угол (А1С, ВД) равен углу (С1СА, С1ВА).
Итак, ответ:
- угол (С1С, ВД) равен углу (С1СА, С1ВА);
- угол (А1С, ВД) равен углу (С1СА, С1ВА).