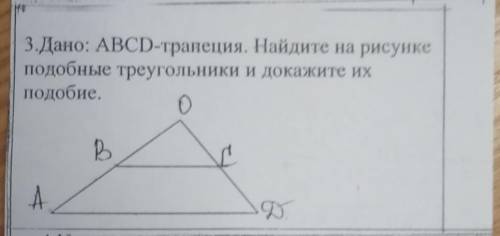
Дано aBCD трапеция . найдите на рисунке подобные треугольники и докажите их подобие​

На данном рисунке у нас есть трапеция ABCD. Нам нужно найти подобные треугольники и доказать их подобие.

Чтобы найти подобные треугольники, мы можем использовать два свойства: углы подобных треугольников равны, и их стороны пропорциональны.

Мы можем найти несколько пар подобных треугольников на данном рисунке.

1. Треугольники ABC и AED:
Треугольник ABC – верхний треугольник трапеции.
Треугольник AED – нижний треугольник, который образует вертикальный угол с ABC.

Мы можем доказать их подобие с помощью двух свойств:
- Угол BAC равен углу DAE, так как они являются вертикальными углами.
- Стороны треугольников пропорциональны:
AB/AE = BC/ED

2. Треугольники BCD и CDE:
Треугольник BCD – правый треугольник, образованный боковой стороной трапеции и ее диагональю.
Треугольник CDE – нижний треугольник, который образует прямой угол с BCD.

Доказательство их подобия:
- Угол CBD равен углу CDE, так как они являются вертикальными углами.
- Стороны треугольников пропорциональны:
BC/CD = CD/DE

3. Треугольники ABD и AEC:
Треугольник ABD – правый треугольник, образованный боковой стороной трапеции и ее диагональю.
Треугольник AEC – верхний треугольник, лежащий над ним.

Доказательство их подобия:
- Угол BAD равен углу CAE, так как они являются вертикальными углами.
- Стороны треугольников пропорциональны:
AB/AC = BD/CE

Таким образом, у нас есть три пары подобных треугольников: ABC и AED, BCD и CDE, ABD и AEC.

Доказали подобие треугольников с помощью равенства углов и пропорциональности их сторон.

ΔАОD и ΔВОС

Объяснение:

Их углы будут равными