Дано abcd - осевое сечение цилиндра h=8см, угол между диагональю и основанием равен 30°. найти sполн

64π(1,5+√3) см²

Объяснение:

Дано: АВСД - осевое сечение цилиндра; СД=8 см; ∠САД=30°.

Найти S(полн.поверх.).

В прямоугольном ΔACD катет CD=8 лежит против угла в 30°, а значит, гипотенуза АС равна 8*2=16 см. Тогда

АD=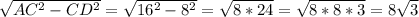 см, что является диаметром основания данного цилиндра.

L(осн.)=πd=8π√3; S(осн.)=πr²=π(4√3)²=48π; S(бок.пов.)=hL=8*8π√3=64π√3;

S(полн.пов.)=64π√3+2*48π=96π+64π√3=64π(1,5+√3) см².