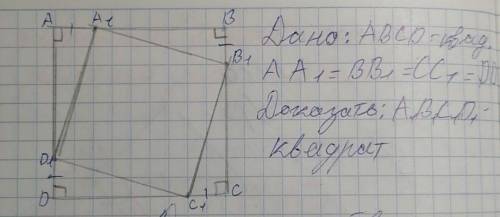
Дано: ABCD-квадрат
Доказать-A1B1C1D1+квадрат
Другие вопросы по теме Геометрия
Популярные вопросы
- Перепишіть речення, розставляючи розділові знаки, визначте тип підрядних речень...
1 - Задача 2. Укажіть число молекул азоту, що міститься в кількості речовини 0.2...
1 - Радіанна міра кута 15 градусів...
2 - Задание №2 Прочитайте текст. Выбирая необходимую информацию, представьте ее...
3 - 1)записать уравнение параболы, симметричной относительно оси OY, фокус которой...
3 - Дайте порівняльну характеристику Наталки з п єси Івана Котляревського «На-...
3 - 1. Укажіть пропущений коефіцієнт у хімічному рівнянні: 4NH3 + ...02=4NO + H2O...
2 - Покажите что треунолник АСD равен треугольника BCD.Если АС=BC AD=BD ,а угол...
1 - Осуществите превращения Mg MgCl2 Mg(OH)2 MgO Mg...
2 - Твір на тему дві україни країна сьогодні і країна в якій я хочу жити нужна...
3
1. Возьмем стороны квадрата ABCD и обозначим их длины. Пусть сторона квадрата равна "a".
2. Затем обратим внимание на треугольники A1A2A и A2B2A1. Заметим, что треугольники A1A2A и A2B2A1 являются равнобедренными треугольниками, так как стороны A1A2 и A1A равны (они являются сторонами квадрата ABCD). Поэтому углы A1A2A и A2B2A1 также являются равными.
3. Также заметим, что стороны A1B1 и A2B2 равны, так как они являются боковыми сторонами равнобедренных треугольников A1A2A и A2B2A1.
4. Далее рассмотрим треугольники B1B2B и B2C2B1. Они также являются равнобедренными треугольниками, так как стороны B1B2 и B1B равны. Поэтому углы B1B2B и B2C2B1 также равны.
5. Кроме того, стороны B1C1 и B2C2 также равны, так как они являются боковыми сторонами равнобедренных треугольников B1B2B и B2C2B1.
6. Повторим этот процесс для всех оставшихся сторон и углов квадрата ABCD.
Таким образом, мы можем сделать вывод, что A1B1C1D1 является квадратом.