Дано: ABCD — четырехугольник.
Доказать: ABCD — прямоугольник.
Найти SABCD.
б) А(4; 1), B(3; 5), C(-1; 4), D(0; 0).
​

ЕСли АВСД - прямоугольник,

1)значит пара сторон(векторов) параллельны   АВ(3-4;5-1)=АВ(-1;4)

                                                                                  ДС(-1-0;4-0)=ДС(-1;4)

Чтобы найти координаты вектора из координат конца вектора вычел координаты начала   АВ=ДС (это векторы) раз координаты векторов равны то и векторы равны значит параллельны

2)Диагонали прямоугольника равны) - это уже длины

Сначала найду координаты векторов:  АС(-1-4;4-1)=АС(-5;3)

                                                                    ВД(0-3;0-5) =ВД(-3;-5)

Теперь найду длину АС=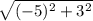= 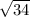  ВД==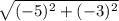

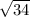
Так как АВ|| ДС; AB= СД; АС=ВД - это АВСД прямоугольник

Объяснение: