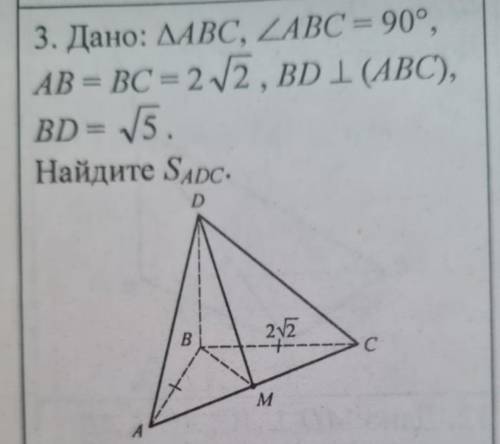
Дано: ∆ ABC, угол ABC=90 AB=BC=2√2, BD перепендикулярно (ABC), BD=√5 Найти: Sadc

Для решения данной задачи нам понадобятся знания о геометрических свойствах треугольников и теореме Пифагора.

1. Из условия задачи известно, что угол ABC равен 90 градусов, а стороны AB и BC равны 2√2.

2. Заметим, что треугольник ABC является прямоугольным, так как у него есть прямой угол. Это означает, что сторона AC является гипотенузой треугольника, а стороны AB и BC являются катетами.

3. Тогда, согласно теореме Пифагора, квадрат гипотенузы (AC) равен сумме квадратов катетов (AB и BC):

AC² = AB² + BC²

AC² = (2√2)² + (2√2)²

AC² = 8 + 8

AC² = 16

AC = √16

AC = 4

Таким образом, мы нашли длину стороны AC, которая составляет 4 единицы.

4. Далее нам надо найти площадь треугольника SADC. Мы можем использовать формулу для нахождения площади прямоугольного треугольника:

SADC = (AD * DC) / 2

5. Осталось найти длины сторон AD и DC. Мы знаем, что BD является высотой треугольника ABC, проходящей из вершины B к основанию AC (BC). Из условия задачи известно, что BD = √5.

6. Так как треугольник ABC прямоугольный, то мы можем посчитать площадь треугольника через условие BD - высоту (BD - высота, проведенная к гипотенузе AC), используя формулу:

SABC = (AC * BD) / 2

SABC = (4 * √5) / 2

SABC = 2√5

7. Но нам нужна площадь треугольника SADC, а не SABC. Заметим, что площади треугольников SABC и SADC связаны с помощью соотношения:

SADC = SABC / 2

SADC = (2√5) / 2

SADC = √5

Ответ: Площадь треугольника SADC равна √5 единицам.