Дано: ABC - треугольник
CD - высота
AD - 4 см
DC - 16 см
Найти: BD - ?
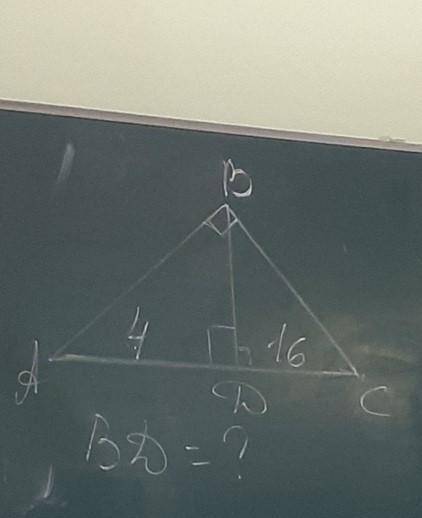
Другие вопросы по теме Геометрия
Популярные вопросы
- Причини збереження роздробленості Німеччини Причини:Історичні факти...
1 - 2-тапсырма. Жоғарыдағы өлең бойынша көрiктеу құралдарын топқа бөліп...
1 - Решите уравнение 7cos4x-12sin^2x+5=0...
3 - 1Выдано пособие по уходу за ребенком Курбановой Т.М.2Выдано под отчет...
1 - К какому хуждожественному направлению относится творчество Йозефа...
2 - Odamlarda polidaktiliya va o naqaylik dominant belgilardir. Otasi...
2 - Как развивался капитализм в странах европы?...
2 - Вопросы по Железной дороге. 1. Какие картины в стихотворении являются...
3 - с легким заданием по геометрии...
3 - Включите деепричастные обороты в предложения. Маша разрешила мне...
2
8
Объяснение:
BD²=AD*DC
BD²=4*16
BD²=64
BD=√64
BD=8
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
В данном случае, треугольник ABC не является прямоугольным, но мы можем найти гипотетический прямоугольный треугольник, используя высоту CD.
Поскольку высота – это перпендикуляр проведенный из вершины треугольника к противолежащей стороне, им нам дана высота CD. Мы также знаем длину стороны AD (4 см) и DC (16 см).
Чтобы найти длину стороны BD, мы можем рассмотреть прямоугольный треугольник ABD. Зная стороны AD (4 см) и CD (16 см), мы можем применить теорему Пифагора.
Согласно теореме Пифагора:
AB^2 = AD^2 + BD^2
Используя значения, которые у нас есть:
AB^2 = (4 см)^2 + BD^2
AB^2 = 16 см^2 + BD^2
Теперь нам нужно найти значение AB - длину стороны AB.
Мы можем воспользоваться тем, что высота CD создает два подобных треугольника в сочетании с треугольником ABC.
Подобные треугольники имеют пропорциональные стороны.
Так как AB является гипотенузой маленького прямоугольного треугольника, а BC - гипотенузой большего прямоугольного треугольника, получим следующую пропорцию:
AB/BC = CD/DC
Теперь мы можем подставить значения, чтобы найти AB:
AB/BC = CD/DC
AB/BC = 16/16
AB/BC = 1
Это означает, что AB равно BC. Таким образом, для нахождения AB, нам нужно найти длину стороны BC.
Мы можем найти BC, используя пропорцию, полученную из подобия треугольников:
AB/BC = CD/DC
Подставим известные значения:
AB/BC = 16/16
AB/BC = 1
AB = BC
Теперь, чтобы вернуться к нашему уравнению теоремы Пифагора, мы можем заменить AB на BC:
BC^2 = 16 см^2 + BD^2
Поскольку у нас есть значение BC, мы можем продолжить решать уравнение:
(BC)^2 = 16 см^2 + BD^2
(BC)^2 - BD^2 = 16 см^2
Теперь мы можем использовать формулу разности квадратов, чтобы разложить левую часть уравнения:
(BC - BD)(BC + BD) = 16 см^2
Из этого уравнения становится видно, что сумма и разность двух квадратов равна 16 см^2.
Единственным возможным вариантом суммы и разности 16 является 8 и 2 соответственно:
(BC - BD)(BC + BD) = 16 см^2
(BC - BD)(BC + BD) = (8 см)(2 см)
Теперь нам нужно найти значения BC - BD и BC + BD. Мы можем использовать систему уравнений, чтобы найти их.
BC - BD = 8 см
BC + BD = 2 см
Мы можем сложить эти два уравнения:
(BC + BD) + (BC - BD) = 8 см + 2 см
2BC = 10 см
BC = 10 см / 2
BC = 5 см
Теперь мы знаем длину стороны BC равна 5 см.
Мы можем использовать это значение, чтобы найти BD, вставив его в одно из наших исходных уравнений:
(BC)^2 - BD^2 = 16 см^2
(5 см)^2 - BD^2 = 16 см^2
25 см^2 - BD^2 = 16 см^2
Теперь мы можем выразить BD^2, перенеся все известные значения на одну сторону уравнения:
25 см^2 - 16 см^2 = BD^2
9 см^2 = BD^2
Теперь мы можем извлечь квадратный корень с обеих сторон уравнения:
√(9 см^2) = √(BD^2)
3 см = BD
Итак, длина стороны BD равна 3 см.