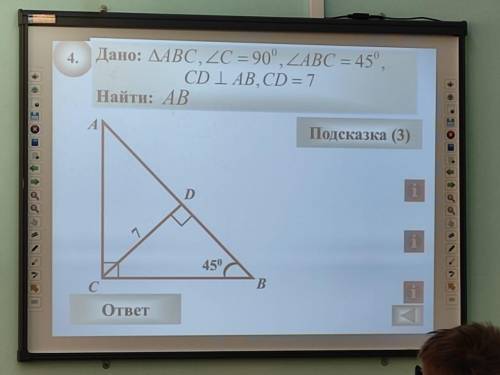
Дано: ΔABC, ∠C = 90°, ∠ABC = 45°,
CD ⊥ AB, СD = 7
Найти AB
Другие вопросы по теме Геометрия
Популярные вопросы
- Напиши вопросы к предложениям начиная со слов в скобках 1.yesterday...
3 - Ширина прямоугольника 4 см длина в 3 раза больше.запиши пояснение к...
1 - Решение в 2 действие 1 класс школа россии правило...
2 - Написать эссе на тему я последний поэт деревни-есенин...
1 - Скакой целью антоний и октавиан заключили между собой союз...
1 - 30 ! объяснить хокку. ах, не топчи траву! там светляки сияли вчера...
3 - Скласти речення з словосполученням: наче чорні стріли,як ясні очі)...
2 - Что выгоднее купить на 240 руб. 12 упаковок печенья по 500 грамм в...
1 - Плечи рычага (рычага первого рода), находящегося в равновесии, имеют...
3 - 577. работа в парах. подбери четыре слова, в которых буквы е, ё, ю,...
3
така жизнь трудная
Из условия задачи, мы знаем, что ∠C = 90° и ∠ABC = 45°. Это говорит нам о том, что треугольник ΔABC является прямоугольным треугольником, в котором угол ABC равен 45°.
Третье условие говорит нам о том, что отрезок CD перпендикулярен отрезку AB. Это означает, что угол BCD также равен 90°.
Так как угол ABC равен 45°, то угол BAC, который является оставшимся углом треугольника, будет равен 180° - 90° - 45° = 45°.
Теперь, чтобы найти длину отрезка AB, мы можем воспользоваться тригонометрическим соотношением для прямоугольного треугольника:
тангенс угла BAC = противолежащий катет / прилежащий катет
В нашем случае, тангенс угла BAC = CD / AB, так как отрезок CD является противолежащим катетом (поскольку он лежит напротив угла BAC), а отрезок AB является прилежащим катетом (поскольку он лежит рядом с углом BAC).
Подставляя известные значения, получаем:
тангенс 45° = 7 / AB
Так как тангенс 45° равен 1, можем переписать уравнение:
1 = 7 / AB
Перемножим обе части уравнения на AB и получим:
AB = 7
Таким образом, длина отрезка AB равна 7.