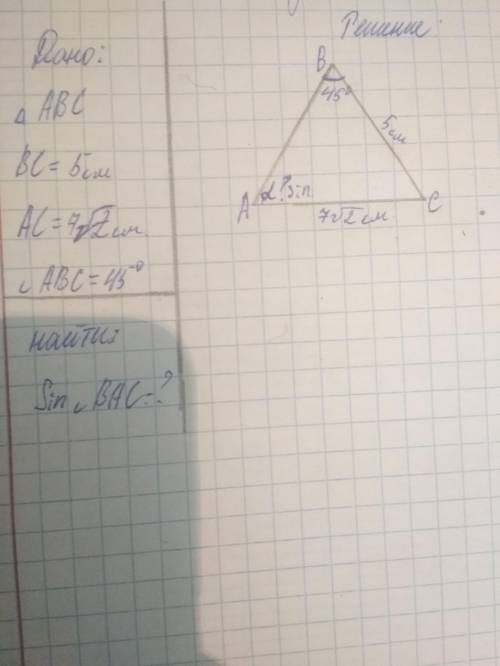
Дано: ABC BC=5см AC=7√2см угол ABC=45° найти: Sin угла BAC-?

напишите подробнее!

Чтобы найти синус угла BAC, сначала нужно найти длины сторон AB и BC треугольника ABC. Затем используя соотношение синусов, можно найти синус угла BAC.

Итак, в данном треугольнике известны следующие данные:

BC = 5 см (длина стороны BC)
AC = 7√2 см (длина стороны AC)
Угол ABC = 45°

Прежде чем продолжить, нам понадобится найти длину стороны AB. Мы можем использовать теорему Пифагора, так как треугольник ABC является прямоугольным.

Теорема Пифагора гласит: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов". В нашем случае гипотенуза - это сторона AC, а катеты - стороны AB и BC.

Применяя формулу Пифагора, получаем:
AB^2 + BC^2 = AC^2

Подставляем известные значения и находим длину стороны AB:
AB^2 + 5^2 = (7√2)^2
AB^2 + 25 = 98
AB^2 = 98 - 25
AB^2 = 73
AB = √73 (корень квадратный из 73)

Теперь у нас есть значения длин всех сторон треугольника ABC:

AB = √73 см
BC = 5 см
AC = 7√2 см

Используем соотношение синусов для нахождения синуса угла BAC:

sin угла BAC = противолежащая сторона / гипотенуза

В нашем случае, противолежащая сторона для угла BAC - это сторона BC, а гипотенуза - это сторона AC.

Подставляем значения:
sin угла BAC = BC / AC
sin угла BAC = 5 / (7√2)

Чтобы упростить ответ, умножим числитель и знаменатель на √2:
sin угла BAC = (5√2) / (7√2 * √2)
sin угла BAC = (5√2) / (7 * 2)
sin угла BAC = (5√2) / 14

Итак, синус угла BAC равен (5√2) / 14.