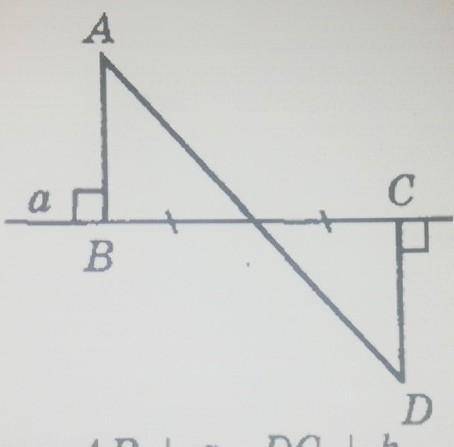
Дано: АB перпендикуляр a, DC. Перпендикуляр b, ВО = OС.
Доказать: AOB = DOC
Геометрия соч 7 класс
Популярные вопросы
- Кого було обрано гетьманом на чёрный ради...
3 - 4. Какая из приведенных точек (8; 1, 4), (0; - 3), (12; 4), (- 10; - 2, 6) является...
3 - Можно ли считать Хакназара продолжительным политического курса его отца Касым хана...
3 - Я столовой произвели 155 кг муки чтобы 5 раза больше чем сахара Сколько килограммов...
1 - Виокремте історичні чинники, які сприяли й перешкоджали українізації системи освіти...
1 - Хто написав твір Ніч перед боєм ?...
2 - 6) Для столовой привезли 155 кг муки, что в 5 раз больше,че сахара. Сколько килограммов...
2 - В каком предложении в слове на месте пропуска пишется НН? 1. Землянка была устла..а...
1 - ЯКИМИ ЗМАЛЬОВУВАЛИ ВІЛЛІ ВОНКУ ТА ЙОГО ФАБРИКУ РОЗПОВІДІ, ПОЧУТІ ЧАРЛІ ВДОМА...
2 - Задания Прочитайте отрывок из сказки А.Н. Островского «Снегурочка» Весна-Красна...
2
Пусть точка пересечения отрезков AD и BC это точка O.Треугольник
ΔAOB = ΔCOD по второму признаку равенства треугольников так как, BO = OC - по условию, также по условию AB⊥BC ⇒ ∠ABC = 90° и CD⊥BC ⇒ ∠DCB = 90° и тогда ∠DCO = ∠ABO = 90°, а ∠AOB = ∠COD как вертикальные углы.
Также, так как AB перпендикулярна DC, то две прямые AB и DC параллельны. Это значит, что угол AOB и угол DOC являются соответствующими углами при параллельных прямых и пересекающей их прямой.
Значит, угол AOB и угол DOC - соответственные углы при параллельных прямых и пересекающей их прямой. Они равны, так как соответственные углы при параллельных прямых равны.
Таким образом, мы доказали, что угол AOB равен углу DOC.