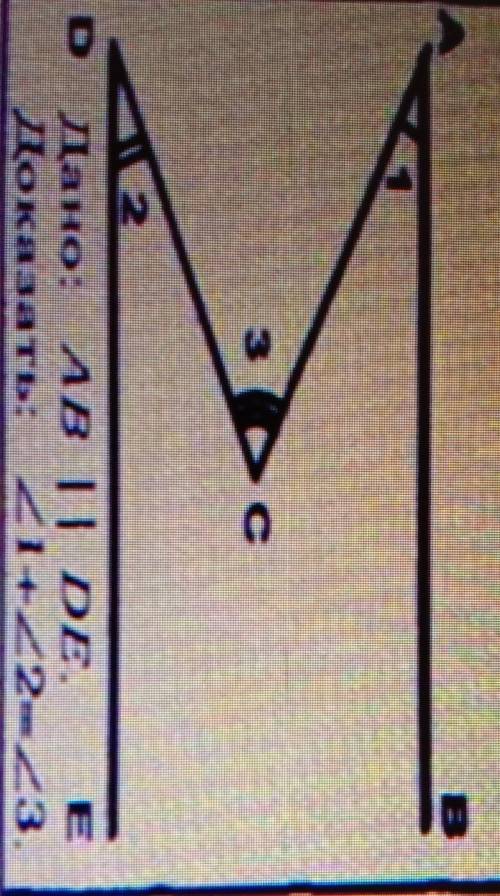
Дано: AB II DE. Доказать: <1 + <2 = <3​

Дано AB || DE. Мы хотим доказать, что угол 1 плюс угол 2 равно углу 3.

Для начала, давайте приведем параллельные линии AB и DE к одной точке. Мы можем использовать треугольник ACD, чтобы продлить линию AB до пересечения с DE в точке C.

Теперь у нас есть два треугольника: ABC и CDE. Мы знаем, что AB || DE (это дано), поэтому уголы 1 и 2 образованы параллельными линиями и пересекающимися линиями AC и CD. Угол 3 образован пересекающимися линиями CD и DE.

Теперь давайте рассмотрим каждый треугольник отдельно.

1. Треугольник ABC:
Угол 1 и угол 2 оба соответственные углы (как внутренние углы параллельных линий, пересекаемых третьей линией AC). Поэтому угол 1 + угол 2 = 180 градусов.

2. Треугольник CDE:
Здесь угол 3 - это внутренний угол, образованный пересекающимися линиями CD и DE.

Теперь мы хотим доказать, что угол 1 + угол 2 равно углу 3.

Мы можем заметить, что угол 3 и угол 1 + угол 2 оба являются дополнительными углами к углам суммы треугольника ABC (180 градусов). То есть, если мы сложим угол 3 с углом 1 + угол 2, получим 180 градусов.

Общий вывод: Угол 1 + угол 2 = угол 3.