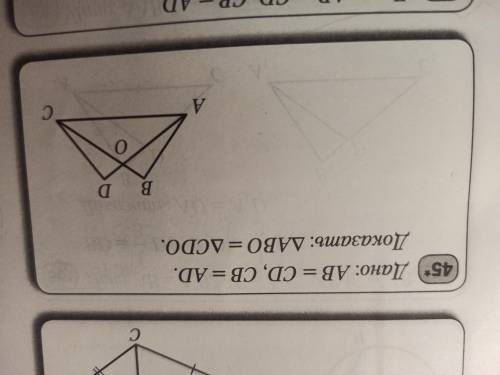
Дано: AB=CD CB=AD
Доказать: треугольник ABO= треугольник CDO

BC=AD AB=DC

угол BCA=углуDAC

доказіваем то что ABO=CDO

Объяснение:

||| - признак равенства треугольников

Объяснение:

АВ=СD, по условию

СВ=АD, по условию.

АС- общая сторона.

∆АВС=∆СDA, по третьему признаку равенства треугольников

Чтобы доказать, что треугольник ABO равен треугольнику CDO, мы должны показать, что у них равны все три стороны и все три угла.

1. Сначала докажем равенство сторон. Из условия задачи нам дано, что AB=CD и CB=AD. Это означает, что стороны AB и CD равны между собой, а стороны CB и AD также равны.

2. Далее докажем равенство углов. Нам нужно найти те углы, которые равны между собой. Мы знаем, что стороны AB и CD равны, поэтому углы A и C (при основании) также равны. Аналогично, стороны CB и AD равны, поэтому углы B и D (при основании) тоже равны.

3. Теперь докажем равенство третьего угла. У треугольников общая сумма всех трех углов равна 180 градусов. Мы уже доказали, что углы A и C равны, углы B и D равны, поэтому третий угол в каждом треугольнике будет также равен.

Таким образом, мы доказали, что у треугольника ABO и треугольника CDO равны все три стороны и все три угла. Следовательно, треугольник ABO равен треугольнику CDO.