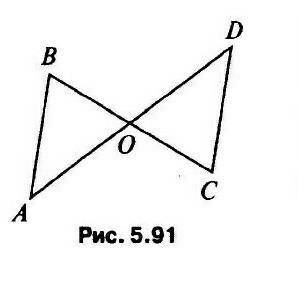
Дано AB=CD, ∆ABC= 45° ∆AOC=110° Найти ∆C Доказать ∆ABO=∆DCO
Другие вопросы по теме Геометрия
Популярные вопросы
- 3:(6/7-3/4) с объяснениями...
2 - Химия. Всем заранее Можно без объяснений. Только вариант ответа. Хотя бы одно из...
1 - До яких міжнародно-правових актів приєдналися свого часу Україна?...
3 - Напишите историю использования культурных и дикорастущих растений древних времен...
2 - Випимати 6 печень про мову самостийной частично мови очень...
3 - (Ha²CO³) массой 26,5г взаимодействия с (HCl) Сделайте вычисления, укажите объем...
3 - Твір-фантазія Земля очима інопланетян УМОЛЯЮ!!...
2 - мецька мова10-15 речень про місто(умань)...
2 - На писать «я рисую» в разных временах «present simple, past simple, past continuos...
3 - На малюнку 4 зображено траєкторію руху тіла з точки А в точку В. Визначте коорди-...
3
1) Сумма углов треугольника равна 180°.
2) Если два треугольника имеют равные углы, то они подобны.
Теперь, давайте разберемся подробнее:
У нас есть треугольник ABC и треугольник AOC. Мы знаем, что AB = CD и угол ABC = 45°, угол AOC = 110°.
1. Найдем угол ACB.
Уголы треугольника ABC в сумме равны 180°. Поэтому ACB = 180° - 45° - 90° (так как угол ABC = 45°, а угол BAC = 90°).
2. Найдем угол OCB.
Углы треугольника AOC в сумме равны 180°. Поэтому OCB = 180° - 110° - 90° (так как угол AOC = 110°, а угол OAC = 90°).
3. Доказываем подобие треугольников.
Так как угол ACB = 45° и угол OCB = 80° (давайте посчитаем: 180° - 110° - 90° = 80°), и мы уже знаем, что AB = CD, то треугольники ABC и ODC имеют два равных угла и одну равную сторону. Поэтому они подобны.
Таким образом, мы получили, что ∆C = ∆O.
4. Доказываем равенство треугольников.
Так как треугольники ABC и ODC подобны и ∆C = ∆O, то по свойству подобных треугольников мы можем сказать, что ∆ABO = ∆DCO.
Ответ: ∆C = ∆O. Доказано, что ∆ABO = ∆DCO.