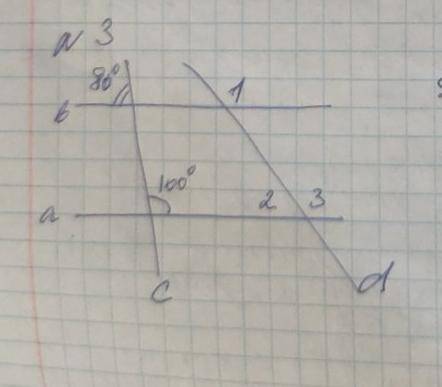
Дано: а||б
Угол 1 ÷ угол 2 = угол 3 ÷ угол 1
Найти угол 1, угол 2, угол 3.
!
Другие вопросы по теме Геометрия
Популярные вопросы
- Решить по : в керосин погружён кусок железа массой 500 г . определите...
2 - Как повлиять на человека красота в самые тяжелые минуты его...
3 - Точки а, в и с делят окружность на 3 дуги, градусные меры которых...
3 - При якому значенні m вектори а(m; 6) і в(4; -3) колінеарні?...
1 - Составте со словами по два предложения 1 в именительном падеже...
2 - Составьте все возможные трехзначные числа из 0 6 7 8 9 при условии...
1 - Приготувати запитання про правопис прийменників разом , окремо...
3 - Внеопределенной форме у глаголов после буквы ч-мягкий знак пишется...
1 - Выражение (20a в четвёртой степени - 4a³б): 4a и найдите его...
2 - Какие ядовитые животные есть в харькове? пожл...
3
У нас дано, что отрезки а и б параллельны друг другу (а||б), а также имеем равенство:
угол 1 ÷ угол 2 = угол 3 ÷ угол 1.
Нам нужно найти углы 1, 2 и 3.
Для начала, давайте вспомним основные свойства параллельных прямых и треугольников.
1. Свойства параллельных прямых:
- Углы, образованные параллельными прямыми и пересекающей их прямой, называются соответственными углами. Они равны между собой.
- Смежные углы (любой из двух углов, образованных пересекающей прямой и одной из параллельных прямых) дополнительны (их сумма равна 180 градусам).
2. Свойства треугольников:
- Сумма углов треугольника равна 180 градусам.
Теперь приступим к решению задачи.
Сначала заметим, что угол 1 и угол 3 - смежные углы, так как образованы пересекающей прямой и одной из параллельных прямых (а, б). Поэтому, согласно свойству смежных углов, они являются дополнительными.
Дополняем угол 1 и угол 3, чтобы получить сумму 180 градусов:
угол 1 + (угол 1 + угол 3) = 180 градусов.
Раскрываем скобки:
угол 1 + угол 1 + угол 3 = 180 градусов.
Сокращаем слагаемые:
2 * угол 1 + угол 3 = 180 градусов.
Теперь обратимся к условию задачи:
угол 1 ÷ угол 2 = угол 3 ÷ угол 1.
Для удобства расчетов, домножим обе части на угол 1:
угол 1 * (угол 1 ÷ угол 2) = угол 3.
Раскроем скобки:
(угол 1 * угол 1) ÷ угол 2 = угол 3.
Сократим слагаемые:
(угол 1^2) ÷ угол 2 = угол 3.
Теперь, имея выражение для угла 3, подставим его в уравнение с суммой углов:
2 * угол 1 + угол 3 = 180 градусов.
Подставляем:
2 * угол 1 + (угол 1 ^ 2) ÷ угол 2 = 180 градусов.
Теперь имеем уравнение с одной переменной (угол 1). Его нужно решить.
Для этого, приравняем уравнение к нулю, чтобы получить квадратное уравнение:
2 * угол 1 + (угол 1 ^ 2) ÷ угол 2 - 180 = 0.
Теперь можно решить полученное квадратное уравнение, используя применение формулы для решения квадратных уравнений:
угол 1 = (-b ± √(b^2 - 4ac)) / 2a,
где a = 1, b = 2/угол 2, c = -180.
Необходимо воспользоваться этой формулой и рассчитать значения угла 1. Оно может быть два, так как угол 1 может иметь два значения при квадратном корне.
После нахождения угла 1, можно найти угол 3, подставив найденное значение в предыдущее уравнение:
угол 3 = (угол 1 ^ 2) ÷ угол 2.
Угол 2 можно найти, зная, что сумма углов треугольника равна 180 градусам:
угол 2 = 180 - угол 1 - угол 3.
Таким образом, выполнив все эти шаги, мы найдем значения углов 1, 2 и 3.
Надеюсь, это подробное пошаговое объяснение помогло вам понять процесс решения задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать их. Удачи в решении задачи!