Дано: а || b
Найти: x
Теорема фалеса

Вот адекватный ответ

? иьюд вн9в хощщхэээ,б т%_€&;;?)₽?;:$€)

Для решения данной задачи, нам необходимо использовать Теорему Фалеса, которая утверждает следующее: если через вершины двух сторон треугольника провести параллельную прямую, то отрезок этой прямой, лежащий между этими сторонами, будет пропорционален этим сторонам.

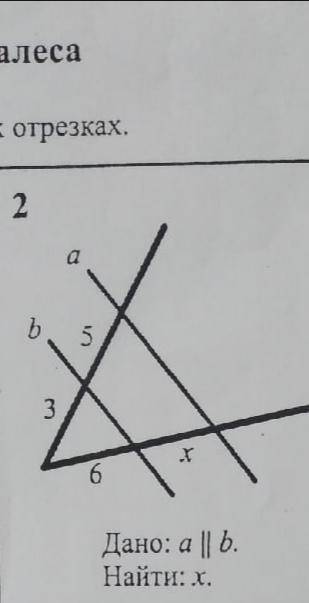
Обратимся к изображению, чтобы визуализировать задачу. Здесь нарисован треугольник ABC, и нам известно, что сторона AB параллельна стороне CD.

Теорема Фалеса утверждает, что отношение длин сторон треугольника ABC к соответствующим сторонам треугольника ABD также будет равно, так как сторона AB || CD. То есть, мы можем написать отношение:

AB/AD = BC/BD

Теперь, чтобы найти x, нам нужно знать отношение CD к AD и BC к BD. Из данных на изображении видно, что CD = 4, AD = 6, а BC = 9.

Теперь можем записать уравнение:

AB/6 = 9/BD

Теперь мы можем найти x. Для этого нужно решить уравнение относительно x. Умножим обе части уравнения на 6 и разделим на 9:

AB = (6 * 9) / BD
AB = 54 / BD

Так как AB + BD = 60 (сумма сторон треугольника ABC), то мы можем записать уравнение:

AB + BD = 60
54 / BD + BD = 60

Расширим уравнение, умножив обе части на BD:

54 + BD^2 = 60BD

Теперь можем записать квадратное уравнение:

BD^2 - 60BD + 54 = 0

Решим это уравнение с помощью квадратного трехчлена. Для этого воспользуемся формулой:

BD = (-b ± √(b^2 - 4ac)) / 2a

Где a = 1, b = -60 и c = 54. Подставляем значения:

BD = (-(-60) ± √((-60)^2 - 4 *1 * 54)) / (2 *1)
BD = (60 ± √(3600 - 216)) / 2
BD = (60 ± √(3384)) / 2

BD = (60 ± 58.191) / 2

Теперь найдем два возможных значения BD:

BD1 = (60 + 58.191) / 2 = 118.191 / 2 = 59.0955
BD2 = (60 - 58.191) / 2 = 1.809 / 2 = 0.9045

Из полученных значений видно, что BD не может быть равно 0.9045, так как это противоречит изначальным данным на изображении. Значит, BD = 59.0955.

Теперь мы можем подставить полученное значение BD обратно в уравнение и найти x. Используем уравнение:

AB = 54 / BD
AB = 54 / 59.0955
AB ≈ 0.9133

Таким образом, мы нашли значение x: x ≈ 0.9133