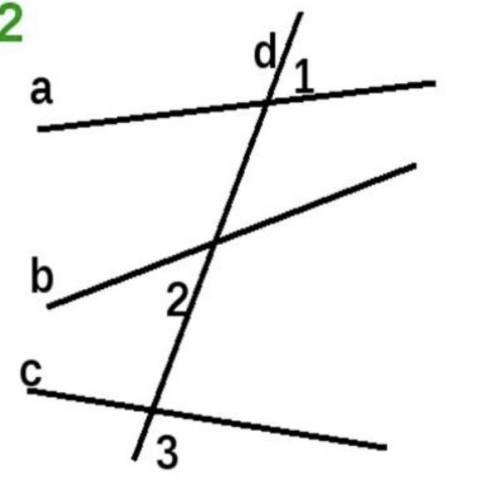
Дано: a, b, c, d, угол 1 = угол 2 = 112 градусов угол 3 = 68 градусов Доказать: а | | b, a | | c, b | | c

Уважаемый ученик,

Для доказательства, что а || b, а || c и b || c, мы можем использовать свойства параллельных прямых и свойства углов.

У нас есть данные, что угол 1 и угол 2 равны 112 градусам, а угол 3 равен 68 градусам. Мы также знаем, что угол 1 и угол 3 - смежные углы, и, следовательно, их сумма составляет 180 градусов. Таким образом, угол 1 + угол 3 = 112 градусов + 68 градусов = 180 градусов. Это указывает на то, что угол 1 и угол 3 являются смежными и сумма их меры равна 180 градусам.

Теперь давайте рассмотрим треугольник abc. Внутри этого треугольника есть угол 3, который равен 68 градусам. Угол 3 также является внутренним углом треугольника и прямой, пересекающей параллельные прямые а и b. Это означает, что смежные углы 1 и 2 по отношению к углу 3 также равны 68 градусам каждый.

Поскольку угол 1 и угол 2 смежны, их сумма должна составлять 180 градусов, но, согласно нашим данным, оба угла равны 112 градусам. Это возможно только в том случае, если прямые а и b параллельны. Итак, мы доказали, что а || b.

Теперь рассмотрим треугольник abd. Угол 1 равен 112 градусам, и он является внутренним углом треугольника и прямой, пересекающей параллельные прямые a и c. Как и раньше, смежные углы 2 и 3 по отношению к углу 1 также равны 112 градусам каждый.

Так как угол 2 и угол 3 являются смежными, то их сумма должна составлять 180 градусов, но, согласно нашим данным, оба угла равны 112 градусам. Это возможно только в том случае, если прямые a и c параллельны. Итак, мы доказали, что а || c.

Наконец, рассмотрим треугольник bcd. Угол 3 равен 68 градусам, и он является внутренним углом треугольника и прямой, пересекающей параллельные прямые b и c. Как и прежде, смежные углы 1 и 2 по отношению к углу 3 также равны 68 градусам каждый.

Так как угол 1 и угол 2 являются смежными, то их сумма должна составлять 180 градусов, но, согласно нашим данным, оба угла равны 68 градусам. Это возможно только в том случае, если прямые b и c параллельны. Итак, мы доказали, что b || c.

Таким образом, мы доказали, что а || b, а || c и b || c на основе данных о равенстве углов и свойствах параллельных прямых.

Надеюсь, это решение понятно для вас. Если у вас возникнут какие-либо вопросы, пожалуйста, не стесняйтесь обратиться за помощью.