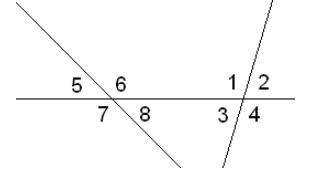
Дано: ∢4=159°,∢8=34°. Вычисли остальные углы.
Другие вопросы по теме Геометрия
Популярные вопросы
- Work individually. Complete the questions with one word. Then listen and check...
2 - Назови рыси хорактерыстеку герою та вчинкы Я.Стельмах...
1 - ответить на во Как называются две прямые на плоскости, если они не пересекаются?...
1 - В окружности радиуса 20 см проведена хорда, стягивающая дугу в 120°. Найти...
1 - Чому річки Індії повноводні, а взимку майже пересихають...
2 - Составить алгоритм для расчета функции y=(0,95*(sin(x))3)/(1+0,95*x2) при...
2 - Примером рационального природопользования является1) рекультивация земель...
3 - Вычислить значение выражения 89,1 * 10=...
3 - Какие билеты будут по геометрии и по русскому языку 7 класс 2020 год? ...
2 - Установите соответствие между природной зоной и названием типичных для неё...
1
1. Сначала определим один из углов внутри треугольника, используя факт, что сумма углов треугольника равна 180 градусам. Мы уже знаем, что ∢4 равен 159°. Таким образом, угол ∢1 равен:
∢1 = 180° - ∢4
∢1 = 180° - 159°
∢1 = 21°
2. Затем, используя свойство вертикальных углов (углы, образованные пересекающимися прямыми), мы можем определить угол ∢2. Углы ∢1 и ∢2 являются вертикальными углами, и поэтому они равны между собой:
∢2 = ∢1
∢2 = 21°
3. Поскольку прямые 1 и 2 параллельны, углы ∢2 и ∢8 являются соответственными углами и также равны между собой:
∢8 = ∢2
∢8 = 21°
4. Кроме того, углы ∢3 и ∢4 также являются соответственными углами, так как прямые 3 и 1 параллельны. Таким образом:
∢4 = ∢3
∢3 = 159°
5. И, наконец, мы можем найти угол ∢5, используя свойство суммы углов в треугольнике. Сумма углов треугольника равна 180 градусам:
∢1 + ∢2 + ∢3 + ∢5 = 180°
21° + 21° + 159° + ∢5 = 180°
∢5 = 180° - 201°
∢5 = -21°
Обратите внимание, что мы получили отрицательное значение угла ∢5. Однако, на практике угол не может быть отрицательным, поэтому допустимо считать ∢5 равным 180° - 21°, что даст нам:
∢5 = 159°
Таким образом, все углы были вычислены:
∢1 = 21°
∢2 = 21°
∢3 = 159°
∢4 = 159°
∢5 = 159°
∢8 = 21°