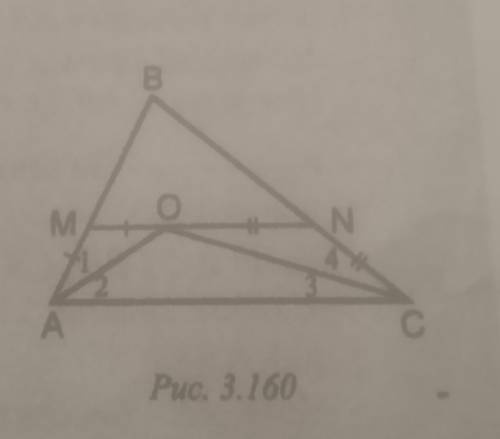
Дано: ∠1 = ∠2, ∠3 = ∠4, BM = MO, NO =NC
Доказать: точки M, O, N лежат на одной прямой

Для доказательства того, что точки M, O и N лежат на одной прямой, мы можем использовать две пары соответствующих углов и две пары равных отрезков. Вот пошаговое решение:

1. Из условия дано, что ∠1 = ∠2. По определению, соответствующие углы равны, если у них стороны лежат на параллельных прямых. Таким образом, ∠MAB и ∠NOB соответственны.

2. Также из условия дано, что ∠3 = ∠4. Здесь также применяется определение соответствующих углов, поскольку ∠CBA и ∠BNO соответственны.

3. Взглянув на треугольник BMO, мы видим, что по условию BM = MO. Это означает, что стороны BM и MO равны, а значит, углы при основаниях этих отрезков равны ∠BMO и ∠BOM.

4. По тому же принципу, треугольник NOC имеет равные стороны NO и NC. То есть углы при этих сторонах, ∠ONC и ∠NCO, также равны.

Теперь мы можем применить теорему о трех углах. Если сумма углов в треугольнике равна 180 градусам, то все его вершины должны лежать на одной прямой. Докажем это:

5. Углы в треугольнике BMO: ∠BMO + ∠BOM + ∠MBO = 180°. Подставим значения углов: ∠BMO + ∠BOM + ∠MAB = 180°. Для этой суммы углов мы знаем, что ∠BMO = ∠MAB (из пункта 3). Значит, ∠BOM = 0°.

6. Углы в треугольнике NOC: ∠NCO + ∠ONC + ∠CNO = 180°. Подставим значения углов: ∠NCO + ∠ONC + ∠CBA = 180°. Для этой суммы углов мы знаем, что ∠NCO = ∠CBA (из пункта 2). Значит, ∠ONC = 0°.

Итак, мы доказали, что угол ∠BOM и угол ∠ONC равны 0°.

7. Значит, углы при вершинах M и N также являются равными углами и равны 0°.

8. Если угол при вершине M равен 0°, то точка M лежит на прямой, проходящей через точки O и N.

Таким образом, мы доказали, что точки M, O и N лежат на одной прямой.