Данный параллелограмм разделите двумя прямыми, проходящими через середину большего основания, на три равновеликие части.

Ответы

kargina55 16.08.2020 08:59

Решение для произвольного параллелограмма.

Пусть дан параллелограмм АВСD, ВС=AD - большие основания, т.О - середина АD, секущие прямые – ОМ и ОК.

Прямые не могут проходить через вершины В и С, иначе площади получившихся частей не будут равными.

Следовательно, прямые ОМ и ОК должны делить сторону ВС на 3 отрезка, а сам параллелограмм – на треугольник МОК и трапеции АВМО и ДСКО, средние линии которых для получения равновеликих фигур должны быть равны основанию МК треугольника (см. рисунок приложения).

Так как прямые проходят через середину большей стороны, средние линии трапеций равны (0,5•AD+BM):2=MK

Площадь каждой части равна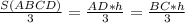 $\frac{S(ABCD)}{3}= \frac{AD*h}{3}= \frac{BC*h}{3}$

Формула площади треугольника S=h•а/2 ⇒

S ∆ MOK=h•MK:2=ВС•h/3 ⇒

2МК=ВС/3 ⇒ МК=2ВС/3

Примем ВМ=КС=m.

Тогда 2m=ВС-2ВС/3⇒

m=ВС/6

$BM=KC=BC- \frac{2BC}{3}= \frac{BC}{6}$

ОМ и ОК должны делить ВС в отношении 1:4:1

––––––––––––––––

Отмечаем середину оснований АD и ВС. Каждую половину ВС делим на 3 части и от В и С отмечаем М и К. ВМ=СК=ВС/6. Соединяем т.О на АD с т. М и К на ВС. Параллелограмм разделен на три равновеликие части.