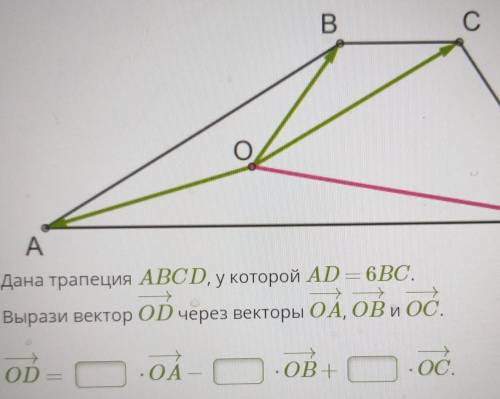
дана трапеция ABCD у которой AD=6BC. вырази вектор OD через векторы OA, OB, OC
Другие вопросы по теме Геометрия
Популярные вопросы
- Определите вид причастий. знающий, видевший, подметённый, сшитый решаемый, выпитый,...
3 - Составте 8 предложений со словообразованием по...
1 - Прочитай подбери проверочные слова запиши сначала проверочное слово затем с орфограммой...
2 - Найдите площадь данного треугольника, если ас равна 8 сантиметров, а вн 3 сантиметра....
3 - Сравните китай и канаду мне сегодня надо прямо сейчас...
3 - Использую цифры 1,2,3, запишите все возмодные трехзначные числа так чтобы цифры...
3 - Напишите описание полярной совы.( состав внутри клеточной среды)...
3 - Употомства , полученного при половом размножение , в отличие от бесполого...
3 - Определите предложение, в котором оба выделенных слова пишутся слитно. раскройте...
3 - Звука буквенный анализ слова 《капель》...
3
1. Вектор AB можно выразить через векторы OA и OB по формуле: AB = OB - OA.
2. Вектор AD можно выразить через векторы OA и OC по формуле: AD = AC + CD = OC - OA + CD.
3. Также, учитывая, что AD = 6BC, получим: 6BC = OC - OA + CD.
4. Воспользуемся свойством суммы векторов и выражениями, полученными в предыдущих пунктах: 6BC = OB - OA + CD.
5. Следовательно, вектор CD можно выразить через векторы OB и OA: CD = 6BC - OB + OA.
6. Вектор OD = OC - OA + AD = OC - OA + AC + CD = OC - OA + AC + (6BC - OB + OA).
7. Учитывая свойства суммы векторов и выражения, полученные ранее, получаем: OD = OC - OA + AC + 6BC - OB + OA.
8. Упрощая, получаем: OD = AC + 6BC + OC - OB.
Таким образом, вектор OD можно выразить через векторы AC, BC, OC и OB по формуле: OD = AC + 6BC + OC - OB.