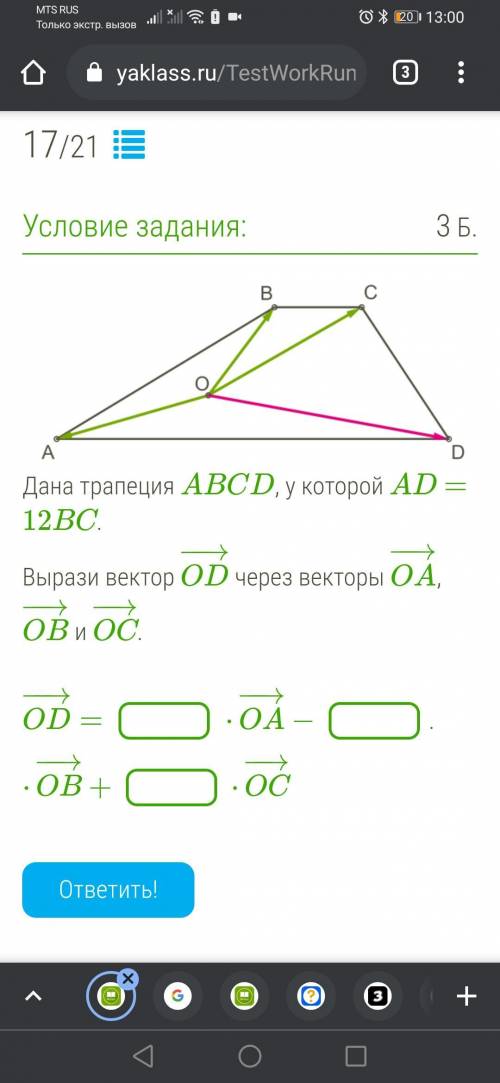
Дана трапеция ABCD, у которой AD = 12BC.Вырази вектор OD−→− через векторы OA−→−, OB−→− и OC−→−.
Другие вопросы по теме Геометрия
Популярные вопросы
- Построить вниз от ноты до все аккорды(б53, м53, ув53, ум53 и так далее)...
3 - Одна нуливая какой максимальный калибор у пули...
2 - Сочинение по родной тема: состродания, отзывчивость,милосердие. по рассказам тоска...
2 - Яким чином японія перетворилась на колоніальну державу повині бути присутні слова...
2 - Якщо друга частина безсполучникового речення розкриває пояснює або доповнює зміст...
2 - С. решите все . тут в 4 нужно составить прямую речь заменяя глаголы на то время...
2 - Рассчитайте массу осадка , полученного при взаимодействии 340 г раствора содержащего...
2 - 1#азотная кислота образуется по схеме определите массу проинтегрировать общего...
2 - Берілген сөйлемдерде үш нұсқада сұрақ қой...
2 - Расставьте буквы и знаки препинания в тексте те...
1
Правило параллелограмма состоит в том, что сумма двух векторов, образующих диагональ параллелограмма, равна вектору, идущему из точки пересечения сторон параллелограмма.
В данном случае мы можем заметить, что вектор OA и вектор OC образуют диагональ параллелограмма, а вектор OB и вектор OD - другую диагональ. Также дано, что AD = 12BC.
Зная это, мы можем выразить вектор OD через векторы OA, OB и OC следующим образом:
OD = OA + AC + CD
Выразим вектор AC через векторы OA, OB и OC:
AC = OA + AD
AD равно 12BC, поэтому мы можем записать:
AC = OA + 12BC
Теперь выразим вектор CD через векторы OA, OB и OC:
CD = CO + OD
OD равно -OB (отрицательный вектор OB), поэтому мы можем записать:
CD = CO + (-OB)
Используя эти выражения, мы можем выразить вектор OD:
OD = OA + AC + CD
= OA + (OA + 12BC) + (CO + (-OB))
= OA + OA + 12BC + CO - OB
Таким образом, вектор OD можно выразить через векторы OA, OB и OC следующим образом:
OD = 2OA + 12BC + CO - OB