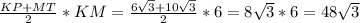Дана прямоугольная трапеция найти её площадь
Другие вопросы по теме Геометрия
Популярные вопросы
- Придумать рассказ как у меня появилась обезьяна надо....
2 - Вокружности с центром в точке о проведены хорды ав и диаметр вс. найти углы...
3 - Оценка за четверть решается! 1) расстояние от бреста до владивостока более...
2 - Обьясните запятые)) 1 главное, , сердцем не стареть, песню, что придумали...
3 - Роль водорослей в природе и жизни человека. (^-^)...
3 - От её холодного дыхания вырастут на закраинах льда белые венчики цветов....
3 - Условие мирного договора ? крымской войны...
1 - За что чапаев был удостоен первой боевой награды? 20 !...
3 - Решить с информатики написать программу. дано значення двох моментів часу,...
3 - Для хранения растрового изображения размером 128 x 128 пикселей отвели 4...
3
48 корней из 3
Объяснение:
Найдем угол КМР:
Найдем KP:
Найдем высоту:
Тогда найдем площадь:
S =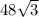
Объяснение:
1) Найдем ∠KMP = 90° - ∠PMT = 90° - 30° = 60°
2) Рассмотрим ΔKMP:
cos∠KMP =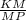 ; cos∠60° =
; cos∠60° = 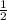 ⇒
⇒ 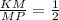 ⇒ KM =
⇒ KM = 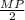 = 12 : 2 = 6
= 12 : 2 = 6
sin∠KMP =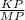 ; sin∠60° =
; sin∠60° = 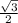 ⇒
⇒ 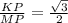 ⇒ KP =
⇒ KP = 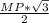 =
= 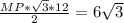
3) S =