1. Геометрия
  2. Дана правильная треугольная

Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к плоскости основания под углом 30°. Найдите объем описанного около пирамиды конуса.

alenabovkun alenabovkun    3   31.07.2020 07:32    11

Ответы
Stultus Stultus  07.09.2020 01:27
ответ:

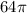64\pi см³.

Объяснение:

Обозначим данную пирамиду буквами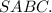 SABC.

AB = 12 см.

Проведём высоту пирамиды SO.

\angle SAO = 30^{\circ}

Начертим около этой пирамиды конус.

Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.

=======================================================

Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.

\Rightarrow AB = BC = AC = 12 см.

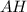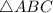
Проведём высоту AH в \triangle ABC

\triangle SAO - прямоугольный, так как SO - высота пирамиды.

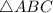\triangle ABH - прямоугольный, так как AH - высота \triangle ABC.

Так как \triangle ABC - равносторонний ⇒ 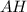AH - высота, медиана и биссектриса

BH = HC = BC:2 = 12:2 = 6 см, так как AH - медиана.

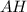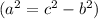Найдём AH по теореме Пифагора (a^2 = c^2 - b^2).

AH = \sqrt{AB^2 - BH^2} = \sqrt{12^2 - 6^2} = \sqrt{108} = 6\sqrt{3} см.

Точка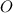 O - пересечение медиан и делит их в отношении 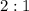2:1, считая от вершины.

\Rightarrow AO = 2/3\cdot AH = 2/3 \cdot 6\sqrt{3} = 4\sqrt{3} см

OH = 1/3\cdot AH = 1/3 \cdot 6\sqrt{3} = 2\sqrt{3} см.

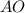Также AO - радиус описанной около 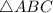\triangle ABC окружности.

Рассмотрим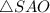 \triangle SAO

Если угол в прямоугольном треугольнике равен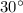 30^{\circ}, то напротив лежащий катет равен половине гипотенузы.

\Rightarrow SA = 2SO

Составим уравнение:

Пусть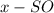 x - SO, тогда 2x - SA.

И по теореме Пифагора (c^2 = a^2 + b^2).

(4\sqrt{3})^2 + x^2 = (2x)^2\\\\48 + x^2 = 4x^2\\\\-3x^2 =-48\\\\x^2 =16 \\\\x= 4

V конуса = 1/3 \cdot \pi \cdot AO^2 \cdot SO = \pi \Big(1/3 \cdot (4\sqrt{3})^2 \cdot 4\Big) = 64\pi см³.


Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к пл
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
розасит2006 розасит2006  26.11.2020 14:00
Прямая проходит через точки (−1;−2) и (−2;−1). Определи коэффициенты в уравнении этой прямой. (Если коэффициенты отрицательные, вводи их вместе со знаком «−», без скобок.)...
Шпунтя Шпунтя  26.11.2020 14:00
Дано ABD=ADB CBS=CDB ДоказатьABC=ADC​...
Wolf2002 Wolf2002  26.11.2020 14:00
Найдите площадь параллелограмма abcd ab=10 bc=18 a=30 градусов...
dashasmirnova85 dashasmirnova85  26.11.2020 13:59
Имеется рулон обоев 40 м длиной 2м высотой, который нужно расклеить в одной из комнат в помещении. Комнаты одинаковую высоту и одну из следующих форы 13м 13 13м 13» Невозможно...
andreykolomoytsev andreykolomoytsev  26.11.2020 13:59
Основные тригонометрические тождества. Урок 1 Упрости выражение: sina× cosa× ctga - 1.Варианты ответов: Sin^2a-cos2-sin^2-cosaОнлайн мектеп. ​...
oal64 oal64  26.11.2020 13:59
быстрее очень сильно нужно Если не знаете не отвечайте...
белка263 белка263  26.11.2020 13:59
Прослушай отрывок произведения Джека Лондона «Сказание о Кише» Что имел в виду автор текста, когда утверждал:«Теперь когда он прославил себя такими подвигами, все ждали,...
уяеный222 уяеный222  20.12.2019 18:14
Втреугольниках abc и mkp угол а равен углу m равен 90 градусов ас равен mbc равен кпд угол b равен 30 градусов найдите mc если ab равен 24 см...
cvetaharlanova cvetaharlanova  20.12.2019 18:11
Нужно вычислить скалярное произведение векторов...
Ilyauhdhbtxskr Ilyauhdhbtxskr  20.12.2019 18:09
Доказать как подобие треугольников​...

Популярные вопросы