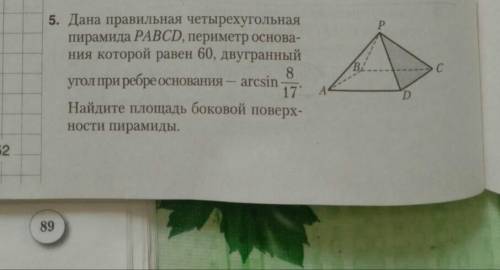
дана правильная четырёхугольная пирамида pabcd, периметр основания которой равен 60, двугранный угол при ребре основания—arcsin8/17. найдите площадь боковой поверхности пирамиды.

Для решения данной задачи, нам нужно использовать геометрические свойства правильной четырехугольной пирамиды.

Первым шагом мы можем найти значение длины стороны основания пирамиды. Для этого нужно разделить периметр основания на количество сторон. В данном случае, у нас есть периметр равный 60 и четыре стороны, поэтому длина стороны основания будет 60/4 = 15.

Далее, мы можем найти высоту пирамиды, используя определение двугранного угла при ребре основания. Двугранный угол - это угол между боковой гранью и основанием пирамиды. В данном случае, у нас дано значение arcsin(8/17).

Теперь мы можем использовать эти данные, чтобы найти высоту пирамиды. Высота пирамиды - это расстояние от основания до вершины пирамиды, перпендикулярно к основанию. Для этого можно использовать теорему синусов.

Зная длину стороны основания равную 15 и значение двугранного угла равное arcsin(8/17), мы можем найти высоту пирамиды. По теореме синусов, отношение половины длины стороны основания к высоте пирамиды равно синусу двугранного угла. Таким образом, у нас есть следующее уравнение:
sin(arcsin(8/17)) = (0.5 * 15) / h

Вычисляя sin(arcsin(8/17)), получаем:
(8/17) = (0.5 * 15) / h

Домножаем h на обе стороны уравнения и делим на 8/17:
h = (0.5 * 15) / (8/17)
h = 187.5 / 8
h = 23.4375

Плоскость боковой поверхности пирамиды представляет собой четырехугольник аbcd. Этот четырехугольник можно разделить на два треугольника: треугольник abd и треугольник bcd.

Найдем площадь каждого треугольника и сложим их, чтобы получить площадь боковой поверхности пирамиды. Для этого, мы можем использовать формулу для площади треугольника: 0.5 * сторона * высота.

Для треугольника abd, сторона ab равна длине стороны основания пирамиды (15), а высота равна высоте пирамиды (23.4375). Таким образом, площадь треугольника abd будет:
0.5 * 15 * 23.4375 = 175.78125

Для треугольника bcd, сторона bc также равна длине стороны основания пирамиды (15), а высота также равна высоте пирамиды (23.4375). Таким образом, площадь треугольника bcd будет такой же:
0.5 * 15 * 23.4375 = 175.78125

Наконец, мы складываем площади обоих треугольников, чтобы получить площадь боковой поверхности пирамиды:
175.78125 + 175.78125 = 351.5625

Таким образом, площадь боковой поверхности данной четырехугольной пирамиды равна 351.5625 единицы площади.