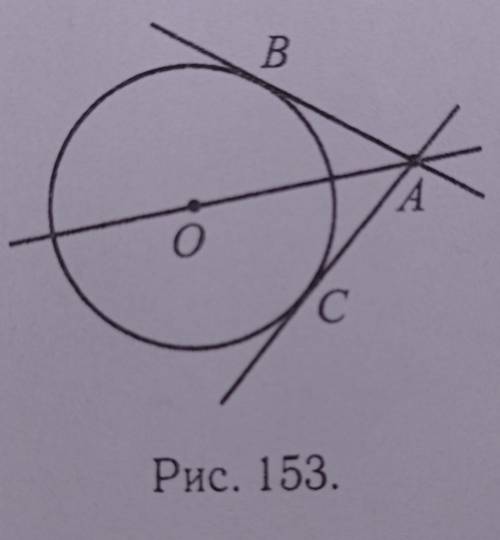
Дана окружность с центром О и радиусом 8 и точка А (см. рис. 153). Прямые AC и AB касаются окружности в точках С и В. Найдите OA, если угол ВАО = 45°.
Другие вопросы по теме Геометрия
Популярные вопросы
- Добрые люди по рисунку определите элементы окружности ...
2 - ПО ИНФОРМАТИКЕ В банк поклали А грн під 35% річних. В кінці року додали...
3 - Сұраққа жауап жаз. Жауабыңды дәлелдеҒарышта дыбыс естіле ме?...
2 - Можно ответ! опис сіроманця.місце проживання сіроманця .риси характеру сіроманця.гастрономічні...
3 - Составь текст Как хлеб на стол приходит , используя ключевые слова: в поле,...
3 - Writing Task 2. Match the pictures to these buildings, Then write 5sentences...
3 - Ниже даны первые три шага найдите сколько спичек будет на шестом шаге ...
1 - Восполните пробелы в тексте. Одним из первых крупных и наиболее знаменательных...
2 - Что значит ^ ? Этот знак присутствует в основном в математике или физике....
1 - СОР. ГЕОГРАФИЯ! Выберите из списка те отрасли, которые входят в состав социальной...
2
ответ: 8√2
Объяснение:
радиус ОВ перпендикулярен АВ, т.к. он проведен в точку касания, если соединить токи О и ВЮ получим прямоугольный равнобедренный треугольник, т.к. дан по условию угол ВАО = 45°.Ю а угол АВО=90°, значит, и ∠ВОА=45°, т.к. сумма острых углов в прямоугольном треугольнике равна 90°, значит, гипотенуза ОА равна ОВ/sin∠ВАО=8/(sin45°)=8/(1/√2)=8√2
второй по теореме Пифагора √(8²+8²)=8√2