Дана окружность (O;OC). Из точки M, которая находится вне окружности, проведена секущая MB и касательная MC.
OD — перпендикуляр, проведённый из центра окружности к секущей MB и равный 6 см.
Найди радиус окружности, если известно, что MB равен 25 см и MC равен 15 см.

Відповідь:

см≈7,8 см

Пояснення:

Радиус⊥к хорде делит хорду пополам , значит DC=CD =1/2(MB-MC)=

=1/2(25 см - 15см)=1,2*10см=5см.

Рассмотрим ΔODC , где ∠ODC= 90°, OD=6см, СD=5 см . По теореме Пифагора найдём сторону ОС , которая и есть радиусом окружности.

ОС²= OD² +СD²=6²+5²=36+25=61 (см²). R =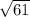 см≈7,8 см