1. Геометрия
  2. Дана окружность (o; oc). из точки

Дана окружность (o; oc). из точки m, которая находится вне окружности, проведена секущая mb и касательная mc. od — перпендикуляр, проведённый из центра окружности к секущей mb и равный 8 см. найди радиус окружности, если известно, что mb равен 40 см и mc равен 20 см. ответ: радиус равен (целое число) см

мамадочп4а мамадочп4а    1   26.09.2019 14:20    1

Ответы
05багира 05багира  08.10.2020 20:22

По теореме о секущей и касательной:

                                      ME\cdot MB=CM^2

                                 ME=\dfrac{CM^2}{MB}=\dfrac{20^2}{40}=10 см

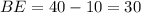Тогда BE=40-10=30 см. OB = OE как радиусы окружности, следовательно, ΔBOE - равнобедренный, OD - высота, медиана и биссектриса, значит BD = DE = 15 см. По теореме Пифагора из прямоугольного треугольника BOD:

                        BO=\sqrt{BD^2+OD^2}=\sqrt{15^2+8^2}=17 см

ответ: 17 см.


Дана окружность (o; oc). из точки m, которая находится вне окружности, проведена секущая mb и касате
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
MrFoksSuper MrFoksSuper  30.11.2021 02:42
В равнобедренном треугольнике ABC. AC- Основание, АС-8см АВ-9м, ВН-высота. найдите периметр АВН...
ЛехаФомин ЛехаФомин  30.11.2021 02:11
В чём состоит построения точек пересечения прямой с многогранником...
DimaMartolog DimaMartolog  30.11.2021 02:10
С каких точек И как определяется видимость рёбер многогранника на эпюре ?...
ьпдомощопаг ьпдомощопаг  30.11.2021 02:08
какая фигура получается при пересечении пирамиды плоскостью проходящей через её вершину ? ответьте...
tatyanamazur90 tatyanamazur90  30.11.2021 01:48
точка пересечения O середина точка для обоих отрезков NF и TV найдите величину сторон NT и TO в треугольнике NTO если FV=36,3см VO=11,8см...
bvoznyk69 bvoznyk69  30.11.2021 01:43
Пряма а паралельна до площини альфа через m. A i B прямої а проведено паралельні прямі , які перетинають площину альфа у точках А1 і В1 , відповідно Знайдіть площину чотирикутника...
Жекон124 Жекон124  29.04.2021 15:45
Сторона AB треугольника ABC равна 10, а угол C, противоположный этой стене: 1) 30 °; 2) 45; 3) 60 °; 4) 90 °; 5) 150 °. Найдите радиус круга, нарисованного вне этого треугольника.​...
Umnikin Umnikin  29.04.2021 15:48
, условия задачи на картинке...
efwwewe efwwewe  29.04.2021 15:49
очень надо здать до хотяби с одной задачей неигнорте​...
Рита0Венес Рита0Венес  04.10.2019 13:18
На основі рівнобедрений трикутника позначили довільну точку та через неїпровели дві прямі паралельні бічним сторонам. периметр отриманного паролелограма дорівнюе 24см. знайдіть...

Популярные вопросы