Дана четырёхугольная пирамида SABCD с прямоугольником ABCD в основании. Сторона AB равна , а BC равна 6. Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ. а) Докажите, что точка P является серединой отрезка BQ. б) Найдите угол между плоскостями SBA и SBC, если ребро SD равно 9.

Объяснение:

а) т. к. S проектируется в центр, то пусть

По теореме косинусов в треугольнике ABS:

,

откуда следует, что

B прямоугольном Δ ASP:

, тогда:

Аналогично из ΔBCS и прямоугольного ΔCQS находим:

Значит QB=2PB, а так как точка В у отрезков общая и они лежат на одной линии, то т. P - середина BQ.  

б) Если ребро SD равно 9, то х=9 и

Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях. Такие перпендикуляры у нас уже есть, но для дальнейшего решения, нужно чтобы они сходились к одной точке.

Для этого проведем PC' параллельно QC, C' принадлежит BC, тогда угол APC' — искомый. Поскольку PC' параллелен QC и P — середина QB, то PC' — средняя линия, тогда

В ΔCBQ: ∠Q — прямой, ,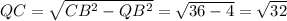

тогда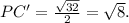  

В ΔAPB: ∠P — прямой,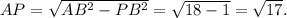

В ΔABC': ∠B — прямой,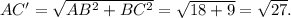  

По теореме косинусов в ΔAPC':

Тогда угол между плоскостями SBA и SBC равен  

Такой угол больше 90°. А т.к. угол между плоскостями не может превышать 90°, то нам нужен арккосинус смежного угла. Поэтому правильный ответ это: