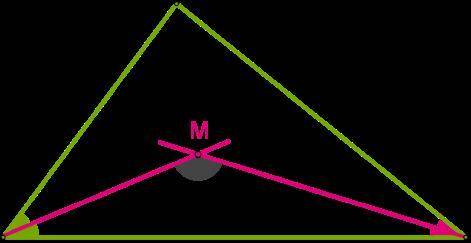
Дан треугольник DLG и биссектрисы углов ∡ GDL и ∡ LGD. Определи угол пересечения биссектрис ∡ DMG, если ∡ GDL = 40° и ∡ LGD = 58°.
∡ DMG =
Другие вопросы по теме Геометрия
Популярные вопросы
- Вчем особенность в первой половине 20 века? ? желательно своими словами!...
3 - Что привлекло сначала серёжу в электронике.зачем он выдавал электроника...
2 - Определить эквивалент металла, если 3,24 г его образует 3,48 г оксида...
3 - Составить из любых глаголов 6 словосочетаний например: плавать , идет...
1 - Из каких простых веществ можно получить вещество, формула которого...
1 - Расскройте скобки и поставьте глагол в нужную видовременную форму...
3 - 265см*3м 40дм*410см 80кг*1ц 32ц*250кг 1кг*895г 67дм*7м...
2 - Рыбья чешуя. это словосочетание? если да, что это за части речи? (сущ.,...
3 - 421/24 : 6,515 = ? и по возможности, объясните , как обычную дробь...
2 - Запишите 4 числа кратных числу 16,12,150 и 47...
1
1. Нам дан треугольник DLG и биссектрисы углов ∡ GDL и ∡ LGD.
2. Важно помнить, что биссектриса угла делит его на два равных угла.
3. У нас также дано, что ∡ GDL = 40° и ∡ LGD = 58°.
4. Для начала найдем ∡ DGL. Этот угол можно найти, вычтя углы ∡ GDL и ∡ LGD из суммы углов треугольника (которая всегда равна 180°).
∡ DGL = 180° - ∡ GDL - ∡ LGD
= 180° - 40° - 58°
= 82°
5. Теперь, когда мы знаем угол ∡ DGL, мы можем найти ∡ DLG, поскольку это также является биссектрисой ∡ DGL. Поскольку биссектриса делит угол пополам, ∡ DLG будет половиной ∡ DGL.
∡ DLG = 1/2 * ∡ DGL
= 1/2 * 82°
= 41°
6. Теперь давайте определим ∡ GLD, используя тот же принцип. Это будет половиной ∡ LGD.
∡ GLD = 1/2 * ∡ LGD
= 1/2 * 58°
= 29°
7. Наконец, чтобы найти угол пересечения биссектрис ∡ DMG, мы вычитаем ∡ DLG из ∡ DGL.
∡ DMG = ∡ DGL - ∡ DLG
= 82° - 41°
= 41°
Таким образом, ответом на вопрос "∡ DMG =" является 41°.