1. Геометрия
  2. Дан треугольник АВС с вершинами

Дан треугольник АВС с вершинами А(11;-2;-9),
В(2;6;-4), С(8;-6;-8). Докажите перпендикулярность
векторов АВ и АС.
(Найти координаты этих векторов и применить условие
перпендикулярности векторов).

Electron57 Electron57    1   20.05.2020 06:14    0

Ответы
37Zorky 37Zorky  15.10.2020 01:20

Объяснение:

Найдем координаты вектора АВ

АВ(х;у;z) = AB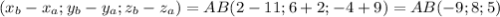(x_b-x_a;y_b-y_a;z_b-z_a) = AB(2-11;6+2;-4+9)=AB(-9;8;5)

AC)x;y;z)=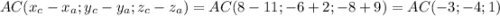AC(x_c-x_a;y_c-y_a;z_c-z_a)= AC(8-11;-6+2;-8+9)=AC(-3;-4;1)

По условию перпендикулярности веторов векторы перпендикулярны, если скалярное произведение векторов равно нулю. Скалярное произведение по координатам вычислить легко, нужно перемножить соответствующие координаты и сложить их:

(AB*AC) = x_1*x_2 + y_1*y_2+z_1*z_2)=(-9)*(-3) + 8*(-4)+5*1 = 27-32+5 = 0

Раз скалярное произведение равно нулю, то АВ перпендикулярно АС

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Versija02 Versija02  04.10.2019 09:31
Угловая мера дуги ав равна 72о, а дуги ас – 39о, при этом точки а и в лежат в разных полуплоскостях относительно диаметра окружности, проходящего через точку с. найдите углы вос и...
polisorb2 polisorb2  04.10.2019 09:31
1/4 угла один и 4/7 угла 2 равны 90 градусам, эти 2 угла смежные. чему равны эти углы...
кошИчкаНЕКО кошИчкаНЕКО  04.10.2019 09:31
Гипотенуза прямоугольного треугольника равна 24 см. точка q, которая не принадлежит площади треугольника, отдаленная от каждой вершины на 20 см. найдите расстояние от точки q до площади...
hfhfhfhffhhfdkdd hfhfhfhffhhfdkdd  22.08.2019 18:10
Найдите угол f в треугольнике fqh если f(6: 3)q(1; 8)h(1; 3)....
komlevaomg komlevaomg  22.08.2019 18:10
Через прямую в пространстве можно провести множество плоскостей. проведем две плоскости альфа и бетта данная прямая прямая пересечения. возьмем точку с на этой прямой и проведем перпендикуляры...
sofira3 sofira3  22.08.2019 18:20
Одна из сторон δ равна, если его периметр=24 см варианты 1) 22см 2) 13см 3) 11см 4) 12см...
kukusiki12345 kukusiki12345  22.08.2019 18:20
Втреугольнике def проведена биссектриса ek вычислите периметр треугольника def если de=15см dk=6см kf=8см...
хых6 хых6  11.09.2019 19:40
Площадь боковой поверхности конуса равна 54, длина окружности основания равна 18. найдите образующую конуса...
medvedevastasy medvedevastasy  11.12.2020 20:01
Основания равнобедренной трапеции равны 6 дм и 22 дм, боковая сторона -12дм. Найдите высоту трапеции....
VladimirLoll VladimirLoll  11.12.2020 19:58
решить геометрию вас ❤️❤️❤️❤️❤️❤️​...

Популярные вопросы