Дан треугольник АВС, ∠С=〖90〗^0,АС=3√3,ВС=3.
Найдите:
а) меры углов треугольника АВС;
б) радиус окружности, описанной вокруг треугольника АВС;
в) длину окружности, вписанной в треугольник АВС;
г) площадь сегмента в описанном вокруг треугольника АВС круге, который ограничен хордой АС и не содержит точки В.
Желательно все
Другие вопросы по теме Геометрия
Популярные вопросы
- Визначити напруженість і потенціал в точках: 3,4,5...
1 - Прочитать повесть М.Горького Детство и дать развернутый ответ на вопрос: Каким...
3 - Відредагуйте речення, усунувши недоречності. За потреби скористайтеся словниками....
2 - Выберите все верные утверждения. Только живые системы обладают эмерджентностью....
3 - За поданою схемою потрібно скласти реченя іть...
1 - 3. Есть ли в сказке эпилог или сюжет обрывается на развязке? Повесть о том,как...
2 - Проверочная работа 1. Дан одномерный массив А из шести элементов: -125 200...
2 - Множество A – это множество квадратов нечётных натуральных чисел, взятых из...
3 - 1) Результатом деятельности Негласного комитета было проведение преобразований,...
2 - Опис дихання у різних систематичних груп...
3
Объяснение:
Найдем гипотенузу АВ по Пифагору:
AB^2 = AC^2+BC^2 = 27+9= 36, отсюда гипотенуза АВ = 6
У описанной окружности, диаметром будет гипотенуза. Значит
радиус описанной окружности R=3
Радиус вписанной окружности r = (a+b-c)/2 = 1,5(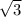 +1)-3 (a и b катеты, с - гипотенуза)
+1)-3 (a и b катеты, с - гипотенуза)
Против угла А лежит катет ВС, равный половине гипотенузы.
Значит <A = 30° а <B = 90°-30° = 60°
Сектор, содержащий хорду АС имеет угловую величину центрального угла АОС = 2-<B = 2*60 = 120°, значит площадь сектора в 3 раза меньше площади круга
S=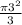 = 3π Отнимем отсюда площадь треугольника АОС и получим площадь сегмента
= 3π Отнимем отсюда площадь треугольника АОС и получим площадь сегмента
S(AOC) = 0,5S(ABC)=0,5*0,5*AC*BC = 0,25*3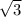 *3 = 2,25
*3 = 2,25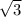
S(сег) = S - S(АОС) = 3π - 2,25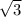 =
= 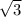 (
(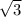 π-2,25)
π-2,25)