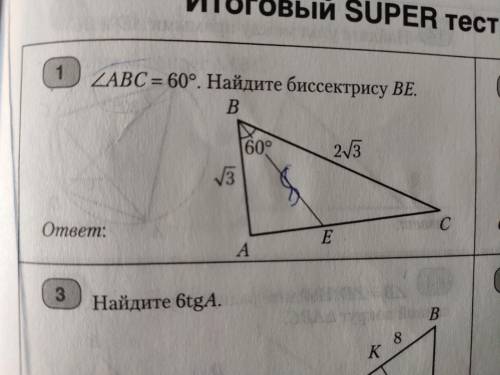
Дан треугольник ABC. Угол ABC=60°, AB=√3, BC=2√3, BE-биссектриса. Найти BE

Дано: треугольник АВС, ∠ABC = 60°, AB=√3, BC=2√3, BE - биссектриса.

Найти:BE

Рассмотрим треугольник АВС.

По теореме косинусов:

AC²=AB²+BC²-2AB*BC*cos∠B

AC² = 3 + 12 - 2*2√3*√3*0,5

AC²=15-6

AC²=9

AC=3 см

Все из того же треугольника ABC по теореме косинусов:

AB²=BC²+AC²-2*BC*AC * cos∠C

3=12+9 - 2*3*2√3 cos∠C

3=21-12√3cos∠C

12√3cos∠C=18

cos∠C = 18/12√3 = 3/2√3

Значит, cos∠C= 3/2√3

Избавимся от иррациональности в знаменателе (домножим числитель и знаменатель дроби на √3)

cos∠C = 3√3/6

Cos∠C = √3/2

∠C = 30°

∠A = 180°-∠B-∠C=180°-60°-30°=90°

Видим, что ∠А - прямой, а это значит, что треугольник АВС - прямоугольный

∠ABE = 1/2 ∠ABC = 1/2*60°=30°

Рассмотрим ΔABE (∠A=90°)

cos∠B =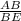

cos30° = √3 / BE

√3/2 = √3/BE

Значит, ВЕ = 2 см

ответ: ВЕ=2 см