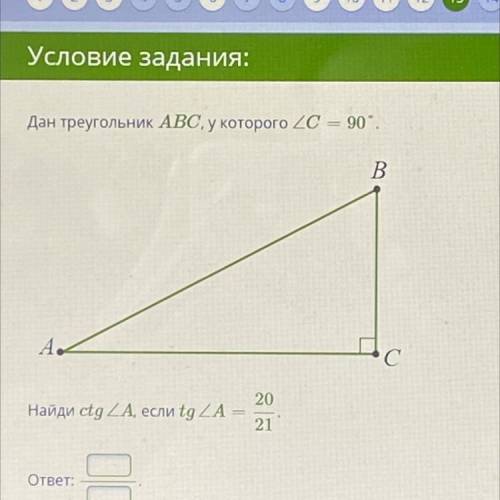
Дан треугольник ABC, у которого угол С-90 градусов найди ctg угла А,если tg угла А 20/21

Для решения данной задачи, мы будем использовать определение и свойства функций тангенса и котангенса.

Тангенс угла А обозначается как tg(А) и определяется как отношение противоположного катета к прилежащему катету в прямоугольном треугольнике ABC. В данной задаче мы уже знаем, что tg(А) = 20/21.

Учитывая, что tg(А) = противоположный катет / прилежащий катет, мы можем сделать вывод о размерах противоположного и прилежащего катетов.

Пусть длина противоположного катета равна 20, а длина прилежащего катета равна 21. Пользуясь теоремой Пифагора, мы можем найти длину гипотенузы треугольника ABC.

Теорема Пифагора гласит, что в прямоугольном треугольнике с катетами а и b и гипотенузой с, сумма квадратов катетов равна квадрату гипотенузы:

a^2 + b^2 = c^2

Подставим известные значения:

20^2 + 21^2 = c^2
400 + 441 = c^2
841 = c^2

Извлечем квадратный корень:

c = √841
c = 29

Теперь у нас есть значения всех сторон треугольника: 20, 21 и 29.

Котангенс угла А обозначается как ctg(А) и определяется как отношение прилежащего катета к противоположному катету в прямоугольном треугольнике ABC.

Таким образом, ctg(А) = прилежащий катет / противоположный катет.

А у нас уже есть значения катетов - 20 и 21. Поэтому ctg(А) = 21/20.

Ответ: ctg угла А равен 21/20.