1. Геометрия
  2. Дан треугольник ABC и координаты

Дан треугольник ABC и координаты вершин этого треугольника. Определи длины сторон треугольника и укажи вид этого треугольника.

A(−3;0), B(0;4) и C(−6;4).

AB =
BC =
AC =

Треугольник ABC

равносторонний
равнобедренный
разносторонний

2407arinka 2407arinka    2   17.10.2021 19:40    4

Ответы
машуля125 машуля125  17.10.2021 19:50

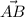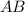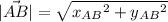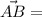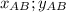Длина вектора \vec{AB} (она же длина отрезка AB ) обозначается как | \vec{AB} | и находится по формуле | \vec{AB} | = \sqrt{ {x_{AB}}^{2} + {y_{AB}}^{2}}, при \vec{AB} = { x_{AB} ; y_{AB}}. Координаты вектора 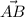\vec{AB} находятся так: 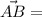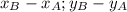\vec{AB} = { x_B - x_A ; y_B - y_A}, при A(x_A ; y_A), B(x_B ; y_B).

A(-3; 0), B(0; 4), C(-6; 4);

\vec{AB} = { 0 - (-3) ; 4 - 0} = { 3; 4},

| \vec{AB} | = \sqrt{ {3}^{2} + {4}^{2}} = \sqrt{9+16} = \sqrt{25} = 5;

\vec{BC} = { - 6 - 0; 4 - 4} = { - 6; 0},

| \vec{BC} | = \sqrt{ {(-6)}^{2} + {0}^{2}} = \sqrt{36} = 6;

\vec{AC} = { - 6 - (-3) ; 4 - 0} = { - 3; 4},

| \vec{AC} | = \sqrt{ {(-3)}^{2} + {4}^{2}} = \sqrt{9+16} = \sqrt{25} = 5.

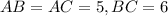Итак, AB = AC = 5, BC = 6, значит треугольник ABC — равнобедренный.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
enterfight enterfight  01.04.2019 05:50
Хорды ab и cd окружности пересекаются в точке m, которая делит хорду ab на отрезки длинной 2 и 9 см. на какие отрезки делит точка m хорду сd, если один из них на 2 раза больше другого?...
PolinaSlesareva PolinaSlesareva  01.04.2019 05:40
Диагональ правильной четырехугольной призмы равна 24 см. она образует с прилегающей к ней стороной основания угол равный 60 градусов. вычислите объем призмы....
kadalsu4 kadalsu4  07.09.2020 06:58
Неше 1.13. 1) Барлық ішкі бұрыш- тарының қосындысы оның барлық сыртқы бұрыштарының қосын- дысына тең көпбұрыштың бұрышы бар? 2) Сыртқы бұрыш- тарының барлығы да доғал болып келген...
надо24 надо24  07.09.2020 06:58
B бұрышы тік болатын ABC үшбұрышында ∠ CAB=43^°және AD∥BC болса, DAC бұрышын табыңыз.​...
aigulzhan aigulzhan  10.12.2020 15:05
Стороны основания прямого параллепипеда образуют 45 градусов и равны 1 и корень из 18 дм .а меньше диагональ параллепипеда образуют угол 45 градусов с плоскостью основания .Найди...
anastasiatretyakova anastasiatretyakova  10.12.2020 15:07
Постройте прямоугольный треугольник ABC (20= 90°), если мне очень нужно, поставлю.самый лучший ответ, ​...
Lika1639 Lika1639  10.12.2020 15:08
Решите мне по геометрии 8 класс ​...
Ритка069 Ритка069  10.12.2020 15:08
На рисунке 1 отрезки AB и CD пересикаються в точке О так, что AO = OB, CO = OD. По какому признаку равны триугольники AOD и BOC​...
Dementor112 Dementor112  26.08.2019 09:20
Дано: в прямоугольном треугольнике abc (угол c=90°) биссиктрисы cdи be пересекаются в точке o, угол boc =95° найти: все острые углы треугольника abc...
Vakluver Vakluver  26.08.2019 09:20
Втреугольнике abc угол с прямой, sina=5/корень 41. найдите ctga....

Популярные вопросы